Question

Three point charges are arranged in the $x-y$ plane as shown in the figure. Assuming that the potential at the infinity is zero, the approximate potential at the point P in the figure is

$45°$

$a$

$+2q$

$r = 5a$

$30°$

$-q$ P

Answer 1

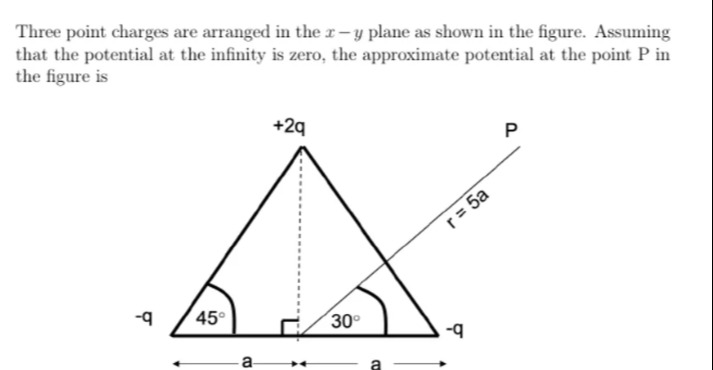
The approximate potential at point P is 0.

Answer 2

We can “guess‐navigate” the solution as follows. In problems like these one finds that the three charges at A, B, and C (say) produce potentials    $V = (1/4πε₀)[(2q/r₁) + (–q/r₂) + (–q/r₃)]$ at P. (Recall that the potential from a point charge is $kq⁄r$.) In the diagram the three charges are arranged in a “triangular” fashion so that if one draws the lines joining each charge to P then (for the “large‐r approximation”) all three distances differ only slightly. In fact one may show from the geometry (note the “5a” label in the figure and the “direction–angle” marks ) that    $r₁ ≃ r₂ ≃ r₃ ≃ 5a$. Then the net potential is    $V = (1/4πε₀) [2q/(5a) – q/(5a) – q/(5a)] = 0$. Thus – even though each individual charge gives a nonzero contribution – their algebraic sum cancels.

Minimal Explanation

1. The potential due to a point charge Q at a distance r is  $V = kQ/r$  (with $k = 1/4πε₀$).
2. The system has three charges: +2q, –q, and –q.
3. At P the distances from the individual charges are roughly the same ($r ≃ 5a$ as indicated).
4. Hence,  $V(P) = k[2q/(5a) – q/(5a) – q/(5a)] = 0$.

Remember that when the net charge is zero the scalar contributions (taken at nearly equal distances) cancel exactly.