Question

Three particles start from the origin at the same time, one with a velocity a, along x-axis, the second along the y-axis with a velocity b and the third along the line $y=x$. The velocity of third particle so that the three may always lie on the same line is
A. $\dfrac{a+b}{2}$
B. $a+b$
C. $\dfrac{\sqrt{2}ab}{a+b}$
D. $\dfrac{ab}{a+b}$

Answer 1

Plot the displacements of each particle in the first second of time on a Cartesian plane. Then assume that the three particles move in a straight line and derive the equation of the line. With the help of the given condition find the x and y coordinates of the third particle to find its velocity.

Formula used:
$m=-\dfrac{b}{a}$
m is slope, b is y-intercept and a is x-intercept of a line.

Complete step by step answer:
It is given that the first particle moves along the x-axis with a velocity ‘a’. Let us assume that all velocities are in the unit of $m{{s}^{-1}}$. Then this means that the particle displaces by a distance of ‘a’ metres on the x-axis in the first second.

Then it is said that the second particle moves along the y-axis with a velocity ‘b’. Therefore, the particle will be displaced by a distance of ‘b’ metres on the y-axis in the first second.
Let the velocity of the third particle be ‘c’. And it is said that this particle moves along the line $y=x$.Therefore, the particle will be displaced by a distance of ‘c’ metres on the line $y=x$ in the first second.Let in a time of 1 second this particle be displaced by distance ‘x’ metres along the x-axis and ‘y’ metres along the y-axis. Therefore, the net displacement of this particle in the first second is $c=\sqrt{{{x}^{2}}+{{y}^{2}}}$ …. (i).

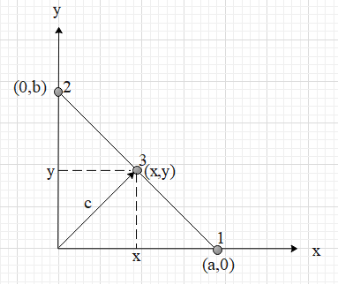
Let us consider that the three particles are always in a straight line. Let the equation of the line be $y=mx+c'$ …. (ii),
where m is the slope of the line and c’ is the y-intercept.
From the figure, we get that the y-intercept is b.
$\Rightarrow c'=b$.
The slope of a line is equal to the negative of the ratio of the y-intercept to the x-intercept.
$\Rightarrow m=-\dfrac{b}{a}$.
Substitute the values of m and c’ in (ii).
$\Rightarrow y=\dfrac{-b}{a}x+b$
$\Rightarrow ay=-bx+ab$.

Since the third is moving on the line $y=x$, substitute $y=x$ in the above equation.
$ax=-bx+ab$
$\Rightarrow x=\dfrac{ab}{a+b}$.
And
$\Rightarrow y=\dfrac{ab}{a+b}$.
But $c=\sqrt{{{x}^{2}}+{{y}^{2}}}$.
$\therefore c=\sqrt{{{\left( \dfrac{ab}{a+b} \right)}^{2}}+{{\left( \dfrac{ab}{a+b} \right)}^{2}}}=\dfrac{\sqrt{2}ab}{a+b}$.
This means that the displacement of the third particle in one second is
$\dfrac{\sqrt{2}ab}{a+b}$ metres. Therefore, its velocity is $\dfrac{\sqrt{2}ab}{a+b}$ $m{{s}^{-1}}$

Hence, the correct option is C.

Note: We used the slope-intercept form of equation of a straight line and found the values of the x and y coordinates of the third particle. However, there are many ways to find x and y coordinates of the particle. We can also write the equation of the line in intercept-intercept form. i.e. $\dfrac{x}{a}+\dfrac{y}{b}=1$, where a and b are the x and y intercepts of the line respectively.