Question

Three particles of masses $1Kg,2Kg,\text{ and }3Kg$ are situated at the corners of the equilateral triangle move at speed $6m{{s}^{-1}},\text{ }3m{{s}^{-1}}\text{ and }2m{{s}^{-1}}$respectively. Each particle maintains a direction towards the particle at the next corner symmetrically. Find velocity of COM of the system at this instant.
$\text{A}\text{. }3m{{s}^{-1}}$
$\text{B}\text{. }5m{{s}^{-1}}$
$\text{C}\text{. 6}m{{s}^{-1}}$
$\text{D}\text{. zero }$

Answer 1

Hint: We will find the position and velocity of the centre of mass by calculating the linear momentum of each particle and their sum divided by the sum of total mass gives the velocity of centre of mass. For calculating the momentum, velocity vector should be considered.
Formula used:

${{\overrightarrow{v}}_{CM}}=\dfrac{{{m}_{1}}{{\overrightarrow{v}}_{1}}+{{m}_{2}}{{\overrightarrow{v}}_{2}}+.....{{m}_{n}}{{\overrightarrow{v}}_{n}}}{{{m}_{1}}+{{m}_{2}}+.....{{m}_{n}}}$

Complete step by step answer:
The centre of mass of a distribution of mass in space is the unique point, an imaginary point in the body of matter, where the weighted relative position of all the distributed masses sums up to be zero. This is the point through which a force may be applied to cause some linear acceleration without an angular acceleration. For simple rigid bodies with uniform density, the centre of mass is located at the centroid. The centre of mass of any system is a point which represents the mean position of the matter in a body or system.
The centre of mass of a system can be calculated by taking the value of all the masses we are trying to find the centre of mass between and multiplying them by their positions. Then, we add these two and divide them by the sum of all the individual masses.
The velocity of the centre of mass is expressed as the sum of momentum of each mass divided by the total mass of the system.

${{\overrightarrow{v}}_{CM}}=\dfrac{{{m}_{1}}{{\overrightarrow{v}}_{1}}+{{m}_{2}}{{\overrightarrow{v}}_{2}}+.....{{m}_{n}}{{\overrightarrow{v}}_{n}}}{{{m}_{1}}+{{m}_{2}}+.....{{m}_{n}}}$
${{\overrightarrow{v}}_{CM}}=\dfrac{{{p}_{1}}+{{p}_{2}}+.....{{p}_{n}}}{{{m}_{1}}+{{m}_{2}}+.....{{m}_{n}}}$

We are given that the three particles of masses$1Kg,2Kg,\text{ and }3Kg$are situated at the corners of the equilateral triangle and moving at speed $6m{{s}^{-1}},\text{ }3m{{s}^{-1}}\text{ and }2m{{s}^{-1}}$respectively.

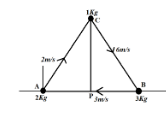
Assume that the point $A$ is origin,

From the figure, $AP=1\times \sin ({{60}^{\circ }})=\dfrac{\sqrt{3}}{2}$

Centre of mass from point$A$in direction of x-axis,

${{x}_{CM}}=\dfrac{{{m}_{A}}{{x}_{A}}+{{m}_{B}}{{x}_{B}}+{{m}_{C}}{{x}_{C}}}{{{m}_{A}}+{{m}_{B}}+{{m}_{C}}}$

${{x}_{CM}}=\dfrac{1\times 0+2\times 1+3\times \dfrac{1}{2}}{1+2+3}=\dfrac{7}{12}$

Centre of mass from point$A$in direction of y-axis,

${{y}_{CM}}=\dfrac{{{m}_{A}}{{y}_{A}}+{{m}_{B}}{{y}_{B}}+{{m}_{C}}{{y}_{C}}}{{{m}_{A}}+{{m}_{B}}+{{m}_{C}}}$
${{y}_{CM}}=\dfrac{1\times 0+2\times 0+3\times \dfrac{\sqrt{3}}{2}}{1+2+3}=\dfrac{\sqrt{3}}{4}$
Coordinates of centre of mass are $\left( \dfrac{7}{12},\dfrac{\sqrt{3}}{4} \right)$
Finding the velocity of centre of mass,

${{\overrightarrow{v}}_{CM}}=\dfrac{{{m}_{A}}{{v}_{A}}+{{m}_{B}}{{v}_{B}}+{{m}_{C}}{{v}_{C}}}{{{m}_{A}}+{{m}_{B}}+{{m}_{C}}}$

${{\overrightarrow{v}}_{CM}}=\dfrac{\text{Total momentum}}{\text{Total mass}}$
Momentum of each particle is the same in magnitude and they are symmetrically oriented, therefore, the total momentum of the system is zero.

${{\overrightarrow{v}}_{CM}}=0$
Hence, the correct option is D.

Note:
While calculating the total momentum of the system, we calculate individual momentum of different masses and add them. For calculating the momentum of different masses, direction of velocity vector should be considered. In this question, it was given that each particle maintains a direction towards the particle at the next corner symmetrically. As a result, sum of individual momentum of masses turned out to be zero.