Question

Three particles of mass 1 kg, 2 kg and 3 kg are placed on the vertices A, B and C of an equilateral triangle. If A and B lie on (0,0) and (1,0) respectively, then the coordinated of the center of mass will be
A. $(\dfrac{{\sqrt 3 }}{2}m\,,\dfrac{7}{6}m)$
B. $(\dfrac{7}{6}\,m,\dfrac{{\sqrt 3 }}{4}m)$
C. $(\dfrac{7}{{12}}m\,,\dfrac{{\sqrt 3 }}{4}m)$
D. $(\dfrac{7}{{12}}\,m,\dfrac{7}{{12}}m)$

Answer 1

A center of mass is that point where the whole mass of the system can be considered to be concentrated. All the weighted position vectors relative to this point sum up to zero. A center of mass is just like another point in the object. It also experiences the same force and undergoes the same acceleration (except for rigid bodies). Here, we shall use the basic formula of center of mass of extended systems. First, we shall calculate the coordinates of point C using various properties of an equilateral triangle and then plug in the value in the formula of center of mass for both x and y directions.

Formula used:
The position of center of mass of a system is given by
${r_{com}} = \dfrac{{{m_1}{r_1} + {m_2}{r_2} + ......... + {m_n}{r_n}}}{{{m_1} + {m_2} + ........ + {m_n}}}$
where $r$ is the position vector.

Complete step by step answer:
Let’s visualize the situation on a cartesian plane.

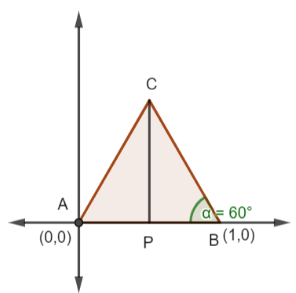
From the figure we can say that $AB = 1\,m$.Since it is an equilateral triangle.All sides must have equal magnitude. Hence, we can say that $AB = BC = AC = 1\,m$.CP is the median and so it bisects AB. So,
$AP = \dfrac{{AB}}{2}$
$\Rightarrow AP = \dfrac{1}{2}\,m$
Now, if we consider $\Delta \,APC$ and apply Pythagoras theorem, we have
$C{P^2} + A{P^2} = C{A^2}$
We know that $AP = \dfrac{1}{2}\,m$ and $AC = 1\,m$

Substituting in the equation we get,
$C{P^2} + \dfrac{1}{4} = 1$
$\Rightarrow C{P^2} = \dfrac{3}{4}$
$\Rightarrow CP = \dfrac{{\sqrt 3 }}{2}\,m$
Now using the basic definition for the position of center of mass of a system which is given by
${r_{com}} = \dfrac{{{m_1}{r_1} + {m_2}{r_2} + ......... + {m_n}{r_n}}}{{{m_1} + {m_2} + ........ + {m_n}}}$ where r is the position vector
In the x direction,
${x_{com}} = \dfrac{{{m_1}{x_1} + {m_2}{x_2} + ......... + {m_n}{x_n}}}{{{m_1} + {m_2} + ........ + {m_n}}}$

As per the given question, the above formula reduces to
${x_{com}} = \dfrac{{{m_1}{x_1} + {m_2}{x_2} + {m_3}{x_3}}}{{{m_1} + {m_2} + {m_3}}}$
Now ${m_1} = 1\,kg\,,\,{m_2} = \,2\,kg\,,\,{m_3} = \,3\,kg$ and the respective positions of x coordinates be ${x_1} = 0\,m\,,\,{x_2} = \,1\,m\,,\,{x_3} = \,\dfrac{1}{2}\,m$
Substituting in the equation, we get,
${x_{com}} = \dfrac{{1 \times 0 + 2 \times 1 + 3 \times \dfrac{1}{2}}}{{1 + 2 + 3}}\,m$
$\Rightarrow {x_{com}} = \dfrac{7}{{12}}m$
In the y direction,
${y_{com}} = \dfrac{{{m_1}{y_1} + {m_2}{y_2} + ......... + {m_n}{y_n}}}{{{m_1} + {m_2} + ........ + {m_n}}}$

As per the given question, the above formula reduces to
${y_{com}} = \dfrac{{{m_1}{y_1} + {m_2}{y_2} + {m_3}{y_3}}}{{{m_1} + {m_2} + {m_3}}}$
Now ${m_1} = 1\,kg\,,\,{m_2} = \,2\,kg\,,\,{m_3} = \,3\,kg$ and the respective positions of y coordinates be ${y_1} = 0\,m\,,\,{y_2} = \,0\,m\,,\,{y_3} = \,\dfrac{{\sqrt 3 }}{2}\,m$
Substituting in the equation, we get,
${y_{com}} = \dfrac{{1 \times 0 + 2 \times 0 + 3 \times \dfrac{{\sqrt 3 }}{2}}}{{1 + 2 + 3}}\,m$
$\therefore {y_{com}} = \dfrac{{\sqrt 3 }}{4}m$
So, the coordinates of center of mass of the system would be $(\dfrac{7}{{12}}m\,,\dfrac{{\sqrt 3 }}{4}m)$.

Hence, option C is the correct answer.

Note: It is not necessary that the center of mass would always be on the geometric center of the body under consideration. For different objects with varied mass distributions, the center of mass is present in different regions of the object. For simplicity, we took the reference to be point A since it was the origin. We could have chosen any of the other two points as well and still get the same answer. This shows that the center of mass does not depend on the frame of reference.