Question

Three particles each having a mass of $m=100\,g$ are placed on the vertices of an equilateral triangle of side $20\,cm$. The work done in increasing the side of triangle to $40\,cm$ is
A. $5\times {{10}^{-12}}J$
B. $2.25\times {{10}^{-10}}J$
C. $4\times {{10}^{-11}}J$
D. $6\times {{10}^{-15}}J$

Answer 1

In order to find the answer of the above question, we will be calculating the work done to assemble the particles on the vertices of an equilateral triangle of sides $20\,cm$. Secondly, we will find the work done to assemble the particles on the vertices of an equilateral triangle of sides $40\,cm$. Finally, we will calculate the difference to reach our correct answer.

Formula used:
Work done: $W=F\cdot d$
Where $F$ is the force due to the gravitational field in this case and $d$ is the relative distance.

Complete step by step answer:
First of all, we will draw a diagram to understand the above question

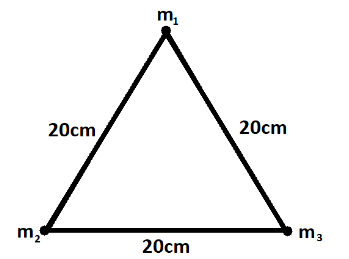
As we can see from the figure, we have three particles having mass $m={{m}_{1}}={{m}_{2}}={{m}_{3}}=100g$placed on the vertices of an equilateral triangle of side $20\,cm$each.

Now we can interpret that, to place these particles on the vertices of this triangle, they are brought here from an infinite distance and placed on the vertices of the triangle. Hence, work is done in bringing those particles from infinite to the vertices.

Therefore, work done to bring the particles from infinite is given by
-When we bring on the first particle, there is no other particle present at that time and hence, the work done to bring the first particle from infinity and place it on one of the vertices is zero and is given by ${{W}_{1}}=0$.

-When we bring the second particle, it will experience a gravitational field due to the first particle and hence work needs to be done against the gravitational field to bring the particle from infinity and place it on one of the vertices and is given by,
${{W}_{2}}=F\cdot d=-G\dfrac{{{m}_{1}}{{m}_{2}}}{{{R}^{2}}}\cdot R=-G\dfrac{{{m}_{1}}{{m}_{2}}}{R}$
The negative sign in the work done is due to the work done in opposition to the gravitational field.

-Similarly, when we bring the third particle from infinity to the vertex of the triangle, it experiences the gravitational field due to the two particles on the other two vertices of the triangle. Hence, work needs to be done against the gravitational fields due to particle one and particle two and is given by
${{W}_{3}}=-G\dfrac{{{m}_{1}}{{m}_{3}}}{R}-G\dfrac{{{m}_{2}}{{m}_{3}}}{R}$
The negative sign in the work done is due to the work done in opposition to the gravitational field.

Therefore, the total work done in assembling the particles on the vertices of the equilateral triangle is given by
${{W}_{tot}}={{W}_{1}}+{{W}_{2}}+{{W}_{3}} \\\ \Rightarrow {{W}_{tot}}=0-G\dfrac{{{m}_{1}}{{m}_{2}}}{R}-G\dfrac{{{m}_{1}}{{m}_{3}}}{R}-G\dfrac{{{m}_{2}}{{m}_{3}}}{R} \\\$
As $m={{m}_{1}}={{m}_{2}}={{m}_{3}}=100\,g$, we can write the above equation as
$\Rightarrow {{W}_{tot}}=0-G\dfrac{m\times m}{R}-G\dfrac{m\times m}{R}-G\dfrac{m\times m}{R} \\\ \Rightarrow {{W}_{tot}}=-3G\dfrac{{{m}^{2}}}{R} \\\$
Now, we have $G=6.67\times {{10}^{-11}}$ (the gravitational constant) and $R=20\,cm$ (the length of the sides of the equilateral triangle)
$\Rightarrow {{W}_{tot}}=-3(6.67\times {{10}^{-11}})\dfrac{(100\times {{10}^{-3}}kg)}{(20\times {{10}^{-2}}m)} \\\ \Rightarrow {{W}_{tot}}=-1.01\times {{10}^{-11}}J$
The above equation gives the work done to bring the particles from infinity to the vertices of an equilateral triangle having sides $20\,cm$.

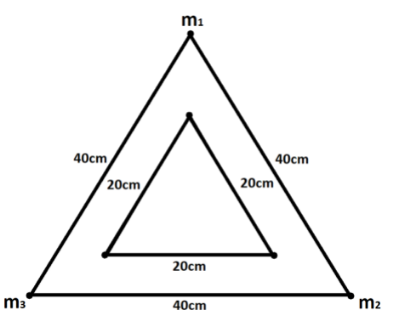
Similarly, the work done to bring the particles from infinity to the vertices of an equilateral triangle having sides $40\,cm$ is given by.
${{W}_{tot}}=-3G\dfrac{{{m}^{2}}}{R} \\\ \Rightarrow {{W}_{tot}}=-3(6.67\times {{10}^{-11}})\dfrac{(100\times {{10}^{-3}}kg)}{(40\times {{10}^{-2}}m)} \\\ \Rightarrow {{W}_{tot}}=-0.505\times {{10}^{-11}}J$

Finally, the work needed to shift the particles from the vertices of the triangle of sides $20cm$to the vertices of the triangle of sides $40\,cm$ is given by

Work done = Total work done in bringing the particles from infinity to the vertices of $40\,cm$ triangle - Total work done in bringing the particles from infinity to the vertices of $20\,cm$ triangle.
$W={{W}_{tot(40)}}-{{W}_{tot(20)}} \\\ \Rightarrow W=(-0.505\times {{10}^{-11}}J)-(-1.01\times {{10}^{-11}}J) \\\ \Rightarrow W=0.50\times {{10}^{-11}}J \\\ \therefore W=5\times {{10}^{-12}}J$
Therefore, the work needed in increasing the side of the triangle from $20cm$to$40cm$is $5\times {{10}^{-12}}J$.

Hence, the correct answer to our question is option A.

Note: It is very important to note that the particles are neutral having equal number of positive and negative charges. If the particles are having some net charge then the work done will also depend upon the electric field produced by the charges in addition to the gravitational field acting on the particles. Therefore, the work done will be the addition of work done due to the gravitational field and the work done due to the electric field.