Question

Three particles each having a charge of $10\mu C$ are placed at the corners of an equilateral triangle of side 10cm. The electric potential energy of the of the system is: (Given $\dfrac{1}{4\pi {{\in }_{\circ }}}=9\times {{10}^{9}}N-{{m}^{2}}/{{C}^{{}}}$ )
a) Zero
b) Infinite
c) 27J
d) 100J

Answer 1

The electric potential energy of a charge distribution is basically due to the work that is done to form the system under the influence or the presence of electric field due to other charges. If a charge is brought into space such that there are no other charges which can interact with the charge, the work done to move the charge in the system is zero. further placing the charge at any point in the presence of other charges work has to be done and therefore accordingly we will determine the energy of the above system.

Formula used:
$E=\dfrac{Qq}{4\pi {{\in }_{\circ }}r}$

Complete step-by-step answer:
Given below is the diagram of the system which is to be assembled.

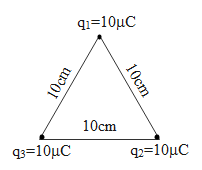
Let us say we wish to bring a particle of charge ‘q’ under the influence of another particle of charge ‘Q’ such that the distance between them is r. Therefore the energy required to bring the particle of charge q at a point r from Q, the work done or the energy of the system is
$E=\dfrac{Qq}{4\pi {{\in }_{\circ }}r}$
Now let us say we bring the first particle of charge ${{q}_{1}}=10\mu C$ in space where we want to form the above triangular system. The energy required or the work done is zero as there is no potential in the region and the charge can be placed anywhere in the space. Further let us say we bring the next charge ${{q}_{2}}=10\mu C$ and place at a distance 10cm from ${{q}_{1}}$ . The work done is,
$\begin{aligned} & {{E}_{1}}=\dfrac{{{q}_{1}}{{q}_{2}}}{4\pi {{\in }_{\circ }}r} \\\ & {{E}_{1}}=\dfrac{{{(10\mu C)}^{2}}}{4\pi {{\in }_{\circ }}10cm} \\\ & \Rightarrow {{E}_{1}}=\dfrac{9\times {{10}^{9}}\times {{10}^{-10}}}{10\times {{10}^{-2}}}J \\\ & \therefore {{E}_{1}}=9J \\\ \end{aligned}$
Now further we bring charge ${{q}_{3}}$ at a distance of 10cm from ${{q}_{1}}$ and ${{q}_{2}}$ to form an equilateral triangle. Now work has to be done in order to overcome the potential of both the charges existing in the system i.e. ${{q}_{1}}$ and ${{q}_{2}}$. Hence the work done to bring the third charge in space to form a triangle is,
$\begin{aligned} & {{E}_{2}}=\dfrac{{{q}_{1}}{{q}_{3}}}{4\pi {{\in }_{\circ }}r}+\dfrac{{{q}_{3}}{{q}_{2}}}{4\pi {{\in }_{\circ }}r} \\\ & {{E}_{2}}=\dfrac{{{(10\mu C)}^{2}}}{4\pi {{\in }_{\circ }}10cm}+\dfrac{{{(10\mu C)}^{2}}}{4\pi {{\in }_{\circ }}10cm} \\\ & \Rightarrow {{E}_{2}}=\left( \dfrac{9\times {{10}^{9}}\times {{10}^{-10}}}{10\times {{10}^{-2}}}+\dfrac{9\times {{10}^{9}}\times {{10}^{-10}}}{10\times {{10}^{-2}}} \right)J \\\ & \therefore {{E}_{2}}=18J \\\ \end{aligned}$
Therefore the total energy (${{E}_{3}}$ )of the above system of triangle is
$\begin{aligned} & {{E}_{3}}={{E}_{1}}+{{E}_{2}} \\\ & {{E}_{3}}=9J+18J \\\ & \therefore {{E}_{3}}=27J \\\ \end{aligned}$

So, the correct answer is “Option C”.

Note: The energy of formation of a system is the same as the energy required to destroy the system. In the above question the equation is valid if the charges are brought from infinity to interact with each other. If there is a sudden formation of charge in space, then the above algorithm does not hold valid.