Question

Three particles A, B and C are thrown with speeds ${v_A},{v_B}$ and ${v_C}$ respectively. A is projected horizontal, B is projected at an angular of $30^\circ$ with the horizontal and C is projected vertically in such a manner that they collide simultaneously at H, the highest point of the parabolic path of B, as shown in the figure. If the acceleration due to gravity is $g$ , then the possible ratio of the speeds ${v_A}:{v_B}:{v_C}$ is –

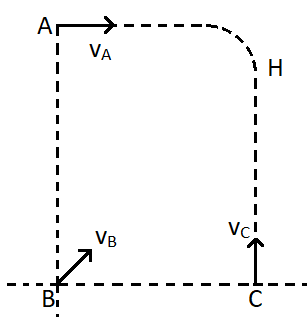
(A) $1:1:1$
(B) $1:2:\sqrt 3$
(C) $\sqrt 3 :1:1$
(D) $\sqrt 3 :2:1$

Answer 1

To solve this problem we need to consider each of the cases separately. We need to find the initial velocities in each case by using separate formulas in the terms of the height $H$ and the acceleration due to gravity. Then on taking the ratio we get the answer.

Formula Used: In this solution we will be using the following formulas,
$\Rightarrow {v^2} = {u^2} + 2gh$
Where $v$ is the initial velocity, $u$ is the initial velocity, $g$ is the acceleration due to gravity and $h$ is the height. And for projectile motion,
$\Rightarrow h = \dfrac{{{u^2}{{\sin }^2}\theta }}{{2g}}$ where $\theta$ is the angle of projection.

Complete step by step answer
To calculate the ratio of the initial velocities in the three cases, we first need to consider the three particles separately.
For the particle A, it is projected horizontally from the height which is also the maximum height of the particle B. Therefore we can consider that the particle A hits the ground making an angle $30^\circ$ with the horizontal.
So for A the initial velocity is only in the $x$ coordinate and the initial velocity along the $y$ coordinate is zero. So on substituting the values in the equation ${v^2} = {u^2} + 2gh$ for the $y$ coordinate we get,
$\Rightarrow {v_y}^2 = 2gH$
On taking root,
$\Rightarrow {v_y} = \sqrt {2gH}$ . This is the final velocity along the $y$ coordinate.
Now for the $x$ coordinate the initial velocity remains as the final velocity. So we get, ${v_x} = {v_A}$
Since the angle made by the final velocity with the horizontal is $30^\circ$ , so we can write,
$\Rightarrow \tan 30^\circ = \dfrac{{{v_y}}}{{{v_x}}}$
Substituting the values we have,
$\Rightarrow \dfrac{1}{{\sqrt 3 }} = \dfrac{{\sqrt {2gH} }}{{{v_A}}}$
So we get the value of ${v_A}$ as,
$\Rightarrow {v_A} = \sqrt 3 \sqrt {2gH}$
Now for the projectile of the particle B, the maximum height is calculated by the formula,
$\Rightarrow h = \dfrac{{{u^2}{{\sin }^2}\theta }}{{2g}}$
So substituting all the values from the question we get,
$\Rightarrow H = \dfrac{{{v_B}^2{{\sin }^2}30}}{{2g}}$
From here we need to find ${v_B}$ so we write,
$\Rightarrow {v_B}^2 = \dfrac{{2gH}}{{{{\sin }^2}30}}$
On taking root and substituting $\sin 30$ as $\dfrac{1}{2}$ we get,
$\Rightarrow {v_B} = 2\sqrt {2gH}$
For the third particle C we will be using the formula, ${v^2} = {u^2} + 2gh$ . Here the final velocity is 0 and the acceleration due to gravity will be $- g$ as the motion is upwards. So substituting we get,
$\Rightarrow 0 = v_C^2 - 2gH$
Therefore, the initial velocity is
$\Rightarrow {v_C} = \sqrt {2gH}$
Thus on taking the ratio we have
$\Rightarrow {v_A}:{v_B}:{v_C} = \sqrt 3 \sqrt {2gH} :2\sqrt {2gH} :\sqrt {2gH}$
Hence we have,
$\Rightarrow {v_A}:{v_B}:{v_C} = \sqrt 3 :2:1$
So the correct answer is option D.

Note
In the question the particle B is undergoing a projectile motion. The projectile motion is the motion where an object is thrown or projected into the air and is subjected only under the acceleration due to gravity. The particle A is also a projectile but is thrown horizontally from a height.