Question
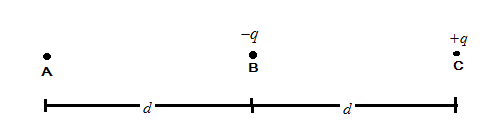
Question: Three particles A, B and C are set in a line, with a distance of \( d \) between each of them, as sh...
Three particles A, B and C are set in a line, with a distance of d between each of them, as shown above. If particle B is attracted more towards particle A, what can we say about the charge qA , of particle A?
(A) qA<q
(B) q<qA<0
(C) qA=0
(D) 0<qA<\+q
(E) qA>+q
Solution
Hint : Here, we have been given the three particles as shown in the figure and we have to compare between the forces on these charges. It can be possible only when we use Coulomb's law and find electrostatic forces between these charges.
Coulomb’s law is given by: F=kd2q1q2
Where, q1 , q2 are the charges on two particles and d is the distance between them.
Complete Step By Step Answer:
Here, three particles are set in the line and particle B is in the influence of two charges from particle A and particle C. To find out the comparison between the charges we have to find out the force exerted by A and C on B by using Coulomb’s law. It is given as:
F=kd2q1q2 …. (1)
It is given that on particle B there is negative charge and this particle B is attracted towards particle A. From this it is clear that A is positively charged.
Now, by using coulomb’s law, electrostatic force between particle A and B is
F=kd2qAq …. (2)
And force between particle B and C,
F′=kd2qq …. (3)
As the particle B is attracted towards A, therefore A exerts a greater force on B than C i.e. F>F′
kd2qAq>kd2qq ….. (From (2) and (3) )
qA>+q
Thus, the charge on A is greater than that of on C, and B is therefore more attracted towards A.
The correct answer is option E.
Note :
It is important to study the significance and application of Coulomb’s law so that we can find out the comparison between charges in this question. We have to understand that the like charges always repel each other so we have seen that the B is attracted towards A it is because the A must be oppositely charged of B.
