Question

Three of six vertices of a regular hexagon are chosen at random. The probability that the triangle with three vertices is equilateral, is equal to

Answer 1

Hint:First of all, find the total number of triangles that is possible by taking 3 points of a regular hexagon which has 6 vertices. Total number of triangles is $^{6}{{C}_{3}}$ . $\Delta DFB$ and $\Delta AEC$are those triangles which have all of three sides equal to each other. So, there are two equilateral triangles possible in a regular hexagon. Probability can be calculated using the formula , $\text{Probability}=\dfrac{\text{total number of equilateral triangles}}{\text{total number of triangles possible}}$.

Complete step-by-step answer:

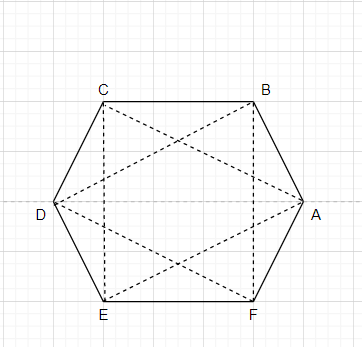
We have connected the vertex A,E and C and can see that we got an equilateral triangle.
Similarly, We have connected the vertex D,F and B and can see that we got an equilateral triangle.
Suppose if we connect the vertex A,D and E, we don’t get an equilateral triangle. Because, according to the diagram we can see that all three sides are not equal to each other.
We have only two equilateral triangles to be formed using a regular hexagon. Out of six points in a hexagon, we have to select only three points at a time.
The total number of triangles to be formed using a regular hexagon=
${}^{6}{{C}_{3}}\ ways$

& =\dfrac{6\times5\times4}{1\times2\times3} \\\ & =\dfrac{120}{6} \\\ & =20 \\\ \end{aligned}$$ Out of 20 triangles, there are only two equilateral triangles that are $$\Delta $$DFB and $\Delta$ AEC. Probability of choosing equilateral triangle $$=\dfrac{2}{20}=\dfrac{1}{10}$$ . Note: In this question, one can make mistakes in taking the number of equilateral triangles. One can think that there can be six equilateral triangles that are $$\Delta DEF$$, $$\Delta DCB$$ , $$\Delta EFA$$ , $$\Delta FAB$$ , $$\Delta CBA$$ and $$\Delta DEC$$. But in these triangles the third side is not equal to the remaining two sides.