Question
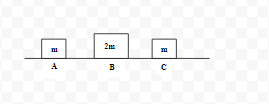
Question: Three objects A, B and C are kept in a straight line on a frictionless horizontal surface. These hav...
Three objects A, B and C are kept in a straight line on a frictionless horizontal surface. These have masses m, 2m and m, respectively. The object A moves towards B with a speed 9m/s and makes an elastic collision with it. Thereafter, B makes a completely inelastic collision with C. All motions occur on the same straight line. Find the final speed (in m/s) of the object C.
Solution
To solve this problem, use the law of conservation of momentum and the maw of conservation of energy. First consider the collision between object A and object B. Use the law of conservation of momentum, substitute the values and get an equation in terms of velocity of both the objects after collision. Then, use the law of conservation of energy. Substitute the values and get an equation. Now, solve both the obtained equations and calculate the velocity of object A and object B. Now, consider the collision between object B and C. As the collision between B and C is inelastic, both the objects move with the same velocity after the collision. Use the law of conservation of energy for this collision and then substitute the values. This will give the final speed of the object C.
Complete answer:
Let uA, uB and uC be the velocity of object A, B and C respectively before the collision
vA, vB and vC be the velocity of object A, B and C respectively after the collision
Given: uA = 9m/s
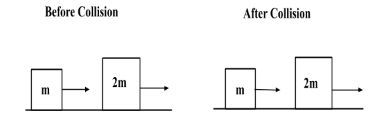
According to law of conservation of momentum, after the collision between object A and object B,
mAuA+mBuB=mAvA+mBvB
Substituting the values in above equation we get,
9m+0=mvA+2mvB
⇒mvA+2mvB=9m
Dividing throughout by m we get,
⇒vA+2vB=9 …(1)
Now, according to the conservation of energy for the collision between object A and object B,
21mAuA2+21mBuB2=21mAvA2+21mBvB2
Substituting the values we get,
21m×92=21mvA2+21×2m×vB2
⇒81m=mvA2+2mvB2
Dividing throughout by m we get,
vA2+2vB2=81 …(2)
Solving equation. (1) and (2) we get,
vA=−3m/s and vB=6m/s
Now, as the second collision is inelastic, after the collision the bodies will move with the same velocity and move as a single body.
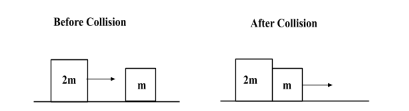
According to law of conservation of momentum, after the collision between object B and object C,
2mvB=2mvC+mvC
Dividing throughout by m we get,
2vB=2vC+vC
⇒2vB=3vC
Substituting value in above equation we get,
2×6=3vC
⇒3vC=12
⇒vC=4m/s
So, the correct answer is “Option C”.
Note:
To solve these types of problems, students should know the difference between elastic collision and inelastic collision. When there is a collision between two bodies and there is no loss of kinetic energy then it is known as Elastic collision. Kinetic energy does not convert into any other form of energy. When there is a collision between two bodies and there is loss of kinetic energy then it is known as Inelastic collision. Kinetic energy gets converted in some other form of energy like heat energy, sound energy, etc. In both the cases, linear momentum and total energy of the system remains conserved.
