Question
Question: Three monkeys A, B, C with masses of 10, 15, 8 kg respectively are climbing up and down the rope sus...
Three monkeys A, B, C with masses of 10, 15, 8 kg respectively are climbing up and down the rope suspended from D. At the instant represented, A is descending the rope with an acceleration of 2m/s2 and C is pulling himself up with an acceleration of 1.5m/s2 . Monkey B is climbing up with a constant speed of 0.8m/s . Treat the rope and monkeys as a complete system and calculate the tension T in the rope at D. (g=10m/s2)
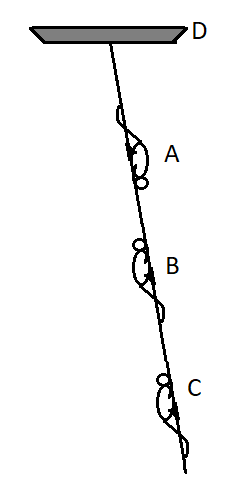
Solution
Hint We need to draw the free body diagrams of each of the monkeys. We consider the tensions for each part of the wire different. Then from the equations of motions of each of the monkeys we need to find the tension at each part. Hence we get the tension at D.
Formula Used: In this solution we will be using the following formula,
⇒Fnet=ma
where Fnet is the net force on the body, m is the mass and a is the acceleration.
Complete step by step answer
Let us consider the monkey C. The forces acting on it are the tension due to the string upwards and the mass of the monkey acting downwards. The monkey C is moving up with an acceleration of 1.5m/s2 .
So the equation of motion of the monkey C will be,
⇒T3−mCg=mCaC
The mass of the third monkey is mC=8kg , g=10m/s2 and the acceleration is ⇒aC=1.5m/s2
Therefore on substituting the values we get,
⇒T3−8×10=8×1.5
So we get the tension as,
⇒T3=(8×1.5)+(8×10)
Hence on calculating e get,
⇒T3=92N
Now for the second monkey B, the forces acting on it are the tension due to the string T2 upwards and the mass of the monkey and the tension T3=92N acting downwards. The monkey B is moving up with a constant speed of 0.8m/s .
So the equation of motion of the monkey B will be,
⇒T2−T3−mBg=mBaB
The mass of the second monkey is mB=15kg , g=10m/s2 and the acceleration is aB=0 since speed is constant. Therefore on substituting the values we get,
⇒T2−92−(15×10)=0
So we get the tension as,
⇒T2=92+150
Hence on calculating e get,
⇒T2=242N
Now for the first monkey A, the forces acting on it are the tension due to the string T1 upwards and the mass of the monkey and the tension T2=242N acting downwards. The monkey A is moving down with a constant acceleration of 2m/s2 .
So the equation of motion of the monkey A will be,
⇒T2+mAg−T1=mAaA
The mass of the first monkey is mA=10kg , g=10m/s2 and the acceleration is aA=2m/s2 Therefore on substituting the values we get,
⇒242+(10×10)−T1=10×2
So we get the tension as,
⇒T1=242+100−20
Hence on calculating e get,
⇒T1=322N
So the tension on the rope at the point D will be T1=322N .
Note
Here we have used the free body diagrams of each of the monkeys to calculate the tension in the string. The free body diagram is a graphical illustration which is used to represent the forces acting on the body and the direction of motion of the body due to the net for acting on it.
