Question

Three mediums of refractive indices ${\mu _1},{\mu _0}{\text{ and }}{\mu _2}$​ are shown in the fig. $\left( {{\mu _1} > {\mu _0},{\text{ and }}{\mu _2} > {\mu _0}} \right)$. The lamps $A$ and $B$ are placed at the bottom and top of the first and third mediums of the same thickness. If the bottom layer of the middle medium is illuminated for a circle of half of the radius for which the upper layer of this medium is illuminated, the relationship between ${\mu _1}{\text{ and }}{\mu _2}$​ is $\left( {given{\text{ }}{\mu _0} = 1} \right)$:

$\left( a \right){\text{ 2}}{\mu _2} = \sqrt {\mu _1^2 + 3}$
$\left( b \right){\text{ }}{\mu _2} = \sqrt {\mu _1^2 + 4}$
$\left( c \right){\text{ }}{\mu _2} = \sqrt {\mu _1^2 + 2}$
$\left( d \right){\text{ }}{\mu _2} = \sqrt {\mu _1^2 + 1}$

Answer 1

Hint First of all by using the formula which is $\operatorname{Sin} c = \dfrac{1}{\mu }$and from this we can now calculate the $\tan {c_1}$ and similarly we will calculate $\tan {c_2}$ and from this we will calculate the radius and them by morphing the distance $r$, we will get the relation between ${\mu _1}{\text{ and }}{\mu _2}$.
Formula used:
By using Snell’s law
$\operatorname{Sin} c = \dfrac{1}{\mu }$, and
$\tan c = \dfrac{1}{{\sqrt {{\mu ^2} - 1} }}$
Here, $\mu$ will be the refractive index.

Complete step by step solution
First of all, we will make the figure from the question and elaborate the figure. Here, by using the Pythagoras theorem we will mark the positions and find the angle between them. The height will be the same in both the mediums.

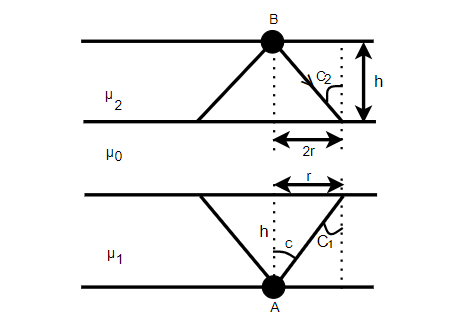
On elaborating the figure, by using the formula $\operatorname{Sin} c = \dfrac{1}{\mu }$and$\tan c = \dfrac{1}{{\sqrt {{\mu ^2} - 1} }}$.
Therefore by using the above, we get
$\tan {c_1} = \dfrac{r}{h}$
And here from the $r$will be given as
$\Rightarrow r = h\tan {c_1}$
Now by substituting the value$\tan c = \dfrac{1}{{\sqrt {{\mu ^2} - 1} }}$, we get
$\Rightarrow r = h \times \dfrac{1}{{\sqrt {\mu _1^2 - 1} }}$, we will let it equation $1$
Now also $\tan {c_2} = \dfrac{{2r}}{h}$
And here from the $r$will be given as
$\Rightarrow 2r = h\tan {c_2}$
Now by substituting the value$\tan c = \dfrac{1}{{\sqrt {{\mu ^2} - 1} }}$, we get
$\Rightarrow 2r = h \times \dfrac{1}{{\sqrt {\mu _2^2 - 1} }}$, we will let it equation $2$
Now on dividing the equation $1$and equation$2$, we get
$\Rightarrow \dfrac{1}{2} = \dfrac{{\sqrt {\mu _2^2 - 1} }}{{\sqrt {\mu _1^2 - 1} }}$
Now on squaring both the sides, we get
$\Rightarrow \dfrac{1}{4} = \dfrac{{\mu _2^2 - 1}}{{\mu _1^2 - 1}}$
So on doing the cross-multiplication, we get
$\Rightarrow \mu _1^2 - 1 = 4\mu _2^2 - 4$
And solving the above equation by removing the square, we get
$\Rightarrow 2{\mu _2} = \sqrt {\mu _1^2 + 3}$
Therefore, the relation between ${\mu _1}{\text{ and }}{\mu _2}$is$2{\mu _2} = \sqrt {\mu _1^2 + 3}$.

Hence, the option $\left( a \right)$is correct.

Note As we have seen that there is a very little bit of concept used for solving this question. The question more emphasizes the calculation and by using the properties of the refraction, we can answer it easily. We just have to use some Pythagoras rule and some trigonometric formulas to solve this.