Question

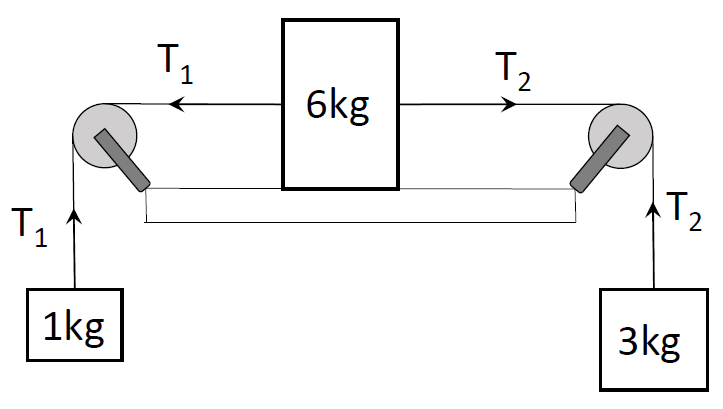
Three masses of 1kg, 6kg and 3kg are connected to each other with threads and are placed on a table as shown in figure. What is the acceleration with which the system is moving?

Answer 1

Hint: If the system starts moving that means there is an unbalanced force to accelerate the system. Assume a variable acceleration and solve for balance of forces for each body in the system. Common forces between the serial bodies are the tension in the cables connecting them.

Complete answer:
As shown in the given figure, the tension in the wire connecting 1kg and 6kg is ${T_1}$ and that in the second wire connecting 6kg and 3kg is ${T_2}$. Let us assume that the pulleys are frictionless and there is no friction between 6kg mass and the board. Therefore, we have the same tension in the wires on both sides of the pulleys. Consider the wires pulling 6kg mass from both sides are horizontal. To solve the problem we will approach each mass in the system separately and draw equations balancing the forces acting on considered mass.
The system will only start to move from rest if there is unbalanced force acting on the masses. Let us consider an acceleration $a$ with which mass 3kg starts moving downwards. Now we considered mass 3kg because it is the larger one amongst the hanging masses. Consider the force balance of 3kg mass knowing that Force = mass times acceleration. Forces acting on the mass is its own weight in downward direction and tension in the upward direction. The resultant between these forces will contribute to the acceleration of this mass as follows:
1. $mg - {T_2} = ma \Rightarrow 3g - {T_2} = 3a$, where $g$ is the acceleration due to gravity.
Now consider the force balance of 6kg mass. The forces acting on the 6kg mass are the tension ${T_1},{T_2}$ each in the opposite direction of the other but in horizontal plane and its own weight in the downward direction balancing normal reaction from the board on which it is held. Therefore there is no acceleration in the vertical direction, and the force balance in the horizontal direction will be:
2. ${T_2} - {T_1} = ma = 6a$
Mass of 1kg is accelerated in the upward direction balancing its own weight in downward direction and the tension in the string in the upward direction. Thus the force balance for this mass will gives us:
3. ${T_1} - mg = ma \Rightarrow {T_1} - g = a$. Since m=1.
Adding all three equations:
$\Rightarrow 3g - {T_2} + {T_2} - {T_1} + {T_1} - g = 3a + 6a + a$
$\Rightarrow 2g = 10a \Rightarrow a = \dfrac{2}{{10}}g$
Now we can generally say this as the final answer. If we consider, for simplicity of number form, $g = 10m{s^{ - 2}}$ instead of $9.8m{s^{ - 2}}$, we get, $a = 2m{s^{ - 2}}$

Note: In the above example, we considered 3kg mass moving in the downward direction with acceleration. We can also start with 1kg mass moving downward with an assumed acceleration. In that case too we will end up with the same figures. You may get a negative sign since you considered 1kg moving downward direction where in actuality, 1kg mass is moving in upward direction.