Question
Question: Three masses m, 2m and 3m are moving in the x-y plane with speeds 3u, 2u and u respectively as shown...
Three masses m, 2m and 3m are moving in the x-y plane with speeds 3u, 2u and u respectively as shown in the figure. The three masses collide at the same point at P and stick together. Find the velocity of the resulting mass?
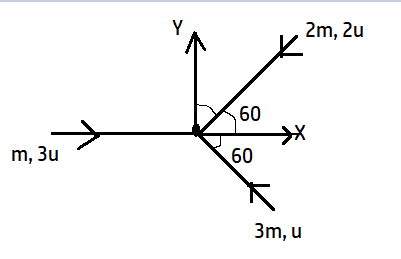
A. 12u(i+3j)
B. 12u(i−3j)
C. 12u(−i−3j)
D. 12u(−i+3j)
Solution
This problem involves collision and there is no loss of energy during the collision. Also, there is no friction present on the ground. It makes a simple problem of energy conservation. We have to also consider the directions since it is of 2-dimension collision.
Complete step by step answer:
We will do this problem by separating components.
For X component:
For first mass:
Mass= m
Velocity= 3u
For second mass:
Mass= 2m
Velocity can be resolved as -2ucos60 = −2u×21=−u
For third mass:
Mass= 3m
Velocity= -ucos60= −u×21=−2u
So, initial x component of linear momentum is m1ux1+m2ux2+m3ux3
