Question
Question: Three long wires, each carrying current are placed parallel to each other. The distance between I an...
Three long wires, each carrying current are placed parallel to each other. The distance between I and II is 3d , between II and III is 4d and between III and I is 5d . The magnetic field at the side of wire II is
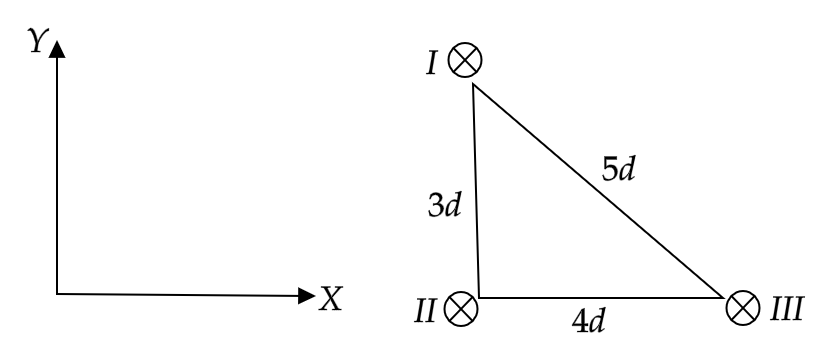
(A) 24πd5μ0i
(B) 24πd10μ0i
(C) 24πd15μ0i
(D) 24πd20μ0i
Solution
In the given question, we have been given an arrangement of current-carrying wires and we have been asked to find the magnetic field at the side of the wire II. Since the magnetic field is a vector quantity, in addition to finding the magnitude of the field caused by the wires, we need to find the direction of the field as well, as we will have to perform vector addition on the obtained magnetic fields to find the net or the resultant magnetic field.
Formula Used: M=2πdμ0i
Complete step by step solution:
To find the direction of the magnetic field due to a current-carrying wire, we will make use of the right-hand rule which states that if the thumb is pointed in the direction of the current, then the direction in which the fingers would curl in the direction of the magnetic field.
According to the right-hand rule, the magnetic field due to III will be upwards and due to I, the magnetic field will be horizontal on the left side.
The magnetic field due to a current carrying wire is given as (M)=2πdμ0i where 2πμ0 is a constant value, i is the current flowing through the wire and d is the length of the wire
The magnetic field in the upward direction will be caused by the wire III, and can be given as
M1=8πdμ0i−−equation(1)
The magnetic field in the left direction is caused by the wire I, and is given as
M2=6πdμ0i−−equation(2)
Since the obtained fields are vector quantities and have specific directions, to find their resultant we will need to find the vector sum of the two magnetic fields calculated above. The vector field is given as the square root of the squares of the magnetic fields, that is
M=(M1)2+(M2)2
Substituting the values in the above equation, we get
