Question
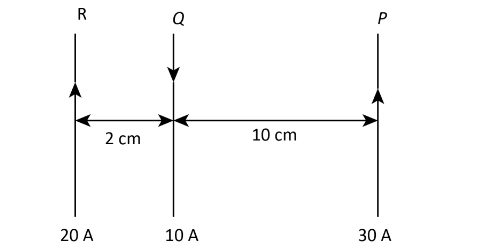
Question: Three long, straight and parallel wires are arranged as shown in figure. The force experienced by ...
Three long, straight and parallel wires are arranged as shown in figure. The force
experienced by 10 cm length of wire Q is
A. 1.4×10−4N toward the right
B. 1.4×10−4N towards the left
C. 2.6×10−4N toward the right
D. 2.6×10−4N toward the left
Solution
Find the magnetic field due to R on Q and due to Pon Q and use this expression to find the force and when the current are in opposite direction in the straight conductor, then the force is repulsive in nature.
Formula used: The magnetic field due to infinitely long straight conductor: B=2πaμ0I
Complete step by step answer:
From the given question, we know that the current in wire P.Q and R are IP=30A, IQ=10A and IR=20A, the distance between the wire
R and Q is aRQ=0.02m, the distance between the wire P and Q is
aPQ=0.1m and the length of the wire Q is L=0.1m
The magnetic field produced by wire R at Q is expressed as,
BRQ=2πaRQμ0IR
Since the force experienced by wire Q is in left direction (repulsion) as the directions of the
current are anti parallel and it is calculated as,
FRQ=IQLBRQ FRQ=IQL2πaRQμ0IR
Similarly, the magnetic field produced by wire P at Q is expressed as,
BPQ=2πaPQμ0IP
Since the force experienced by wire Q is in right direction (repulsion) as the directions of the
current are anti parallel and it is calculated as,
FPQ=IQLBPQ FPQ=IQL2πaPQμ0IP
The net force experienced by the wire Q is calculated as,
F=FRQ−FPQ =IQL2πaRQμ0IR−IQL2πaPQμ0IP =2πIQLμ0[aRQIR−aPQIP] =2π10×0.1×4π×10−7[0.0220−0.130] =1.4×10−4Ntowardsright
Thus, the force experienced by the wire Q is 1.4×10−4N toward right
direction and option (A) is correct.
Note: Be careful while answering, because the formula for finite straight wire and infinite
straight are completely different.
When wire has finite length: B=4πaμ0I(sinϕ2+sinϕ1)
When wire has infinite length, ϕ1=ϕ2=90∘: B=2πaμ0I
When wire has infinite length and point P lies at near wire’s end, ϕ1=90∘andϕ2=0:
B=4πaμ0I
