Question
Question: Three large plates are arranged as shown. How much charge will flow through the key \(K\) if it is c...
Three large plates are arranged as shown. How much charge will flow through the key K if it is closed ?
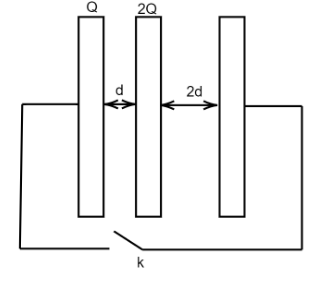
Solution
The figure shows that these three plates of the capacitors are connected with each other, this means that these three plates are connected in parallel.As we know that in parallel combination, the potential difference on the capacitors is the same.
Formula used:
C=VQ
[C=capacitance in Farads, Q= Charge in Coulombs, V=Potential difference in Volts]
C1q1=C2q2
C=dε0A
[ C=capacitance in Farads,ε0 = permittivity of free space, A= area of one plate in square meters, d=distance between the two plates in meters]
C2C1=d2d1
Complete step by step answer:
Capacitors are the devices that store the charge on them. Their ability to store the charge on them is represented by capacitance. It is calculated as
C=VQ −(1)
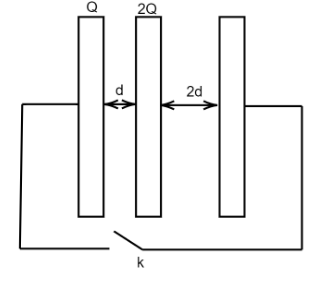
The above plates can be divided into two capacitors, we can show them as
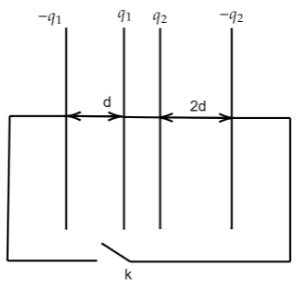
As we can see, both plates of the capacitors are connected together; this means that they are connected in parallel. In parallel combination, the potential difference is the same. Therefore,
V1=V2
From eq (1)
C1q1=C2q2 -(2)
The capacitance of a parallel plate capacitor depends on the dimensions of the capacitor as-
C=dε0A −(3)
ε0and A are constants, therefore, from eq (3),
C2C1=d2d1
Substituting values from the above equation, we get,
C2C1=d2d
⇒C1=2C2 -(4)
Substituting eq (4) in eq (2),we get
C1q1=C2q2
⇒2C2q1=C2q2
∴q1=2q2
We know that,
q1+q2=2Q
⇒2q2+q2=2Q
⇒3q2=2Q
∴q2=32Q
q2has the value q2=32Q, therefore, q1will have the value-
q1=2q2
⇒q1=2×32Q
∴q1=34Q
Therefore, the charge on the first capacitor is32Q and the charge on the second capacitor is 34Q. The charge that flows through the wire when the key is closed is
−q1−(q1)=−q2+q1
∴3−4Q+32Q=−32Q
Therefore, the charge that flows through the wire when the key is closed is 32Q.
Note: The negative charge on the charge that flows through the circuit indicates that this charge flows opposite to the flow of current. In series, the charge is the same on the capacitors, while in parallel, the potential drop on the capacitors is the same. The permittivity of a material is its ability to store electrical energy in an electric field.
