Question
Question: Three infinitely charged sheets are kept parallel to x-plane having charge densities as shown. Then,...
Three infinitely charged sheets are kept parallel to x-plane having charge densities as shown. Then, the value of the electric field at 'P' is
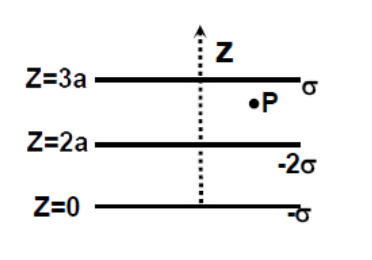
A. ε0−4σk^
B. ε04σk^
C. ε0−2σk^
D. ε02σk^
Solution
For an infinitely charged plane sheet, electric field is given by E=2ε0σ .
The total electric field at point ‘P’ will be the vector sum of the electric field due to all the three infinitely charged sheets.
Complete answer:
As given in the question, three infinitely charged sheets are kept parallel to x-plane or are kept at z=0,z=2a, and z=3a.
For an infinite sheet of charge, the electric field will be perpendicular to the surface and given by E=2ε0σ. This formula is derived by the Gauss Law which states that the total electric flux out of a closed surface is equal to the charge enclosed divided by the permittivity. The electric flux in an area is defined as the electric field multiplied by the area of the surface projected in a plane and perpendicular to the field.
Now, the direction of the electric field depends on the sign of surface charged density σ and the location of the point P. If σ is positive then the direction will be towards point P.
Let us suppose an upward direction to be positive.
So, the electric field due to the sheet at z=0, E−σ=−2ε0σ
Similarly, the electric field due to the sheet at z=2a, E−2σ=−2ε02σ.
And, the electric field due to the sheet at z=3a, Eσ=−2ε0σ
Now, the total electric field due to the sheets at point P is given by, EP=E−σ+E−2σ+Eσ as a vector sum.
So, EP=−2ε0σ−2ε02σ−2ε0σ
On simplification we have, EP=−ε02σ
Here (–) sign represents the downward or opposite of k^.
∴ The the value of electric field at 'P' is EP=−ε02σ. Hence, the correct option is (C).
Note:
The electric field is a vector quantity. So, carefully determine the direction of the field. Remember that the direction of the electric field depends on the sign of surface charge density σ and the location of the point P. If σ is positive then the direction will be towards point P and if it is negative then the direction will be away from point P.
