Question

Three identical thin rods, each of mass m and length l, are joined to form an equilateral triangle. Find the moment of inertia of the triangle about one of its sides.
$\left( A \right)\dfrac{{M{L^2}}}{2}$
$\left( B \right)\dfrac{{M{L^2}}}{3}$
$\left( C \right)\dfrac{{M{L^2}}}{9}$
$\left( D \right)\dfrac{{M{L^2}}}{{12}}$

Answer 1

The sum of moment of inertia of each rod is the moment of inertia of the system. As the distance is zero the rod at the axis will not have the moment of inertia. Calculate the moment of inertia on each side of a triangle. This will help to solve the question.

Complete step by step solution:
The sum of moment of inertia of each rod is the moment of inertia of the system. When a body is undergoing rotational motion only then we talk in terms of moment of inertia. The value of torque will be greater and is required to interrupt its present state when the moment of inertia is greater.

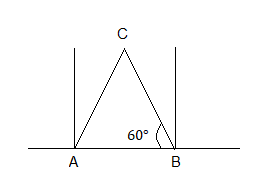
First let us find the moment of inertia of the system. The sum of moment of inertia of each rod is the moment of inertia of the system.
$MI = {I_{AB}} + {I_{BC}} + {I_{CA}}$
Here we can see in the figure that the rod AB is perfectly at the axis hence the moment of inertia is zero.
$\Rightarrow MI = \dfrac{1}{3}M{L^2} = 0$
In the similar way BC and AC have the same kind of arrangement about the axis. Therefore
$MI = \dfrac{1}{3}ML_{eff}^2$
Here the ${L_{eff}}$ is the effective length and the perpendicular length to the axis
$\Rightarrow {L_{eff}} = L\sin \theta$
Where $\theta$ is the angle of equilateral triangle
$\Rightarrow \theta = {60^0}$
$\Rightarrow {L_{eff}} = L\sin {60^0} = \dfrac{{\sqrt 3 L}}{2}$
The moment inertia of the rod BC
$\Rightarrow MI = \dfrac{1}{3}ML_{eff}^2$
$\Rightarrow MI = \dfrac{1}{3}M{\left( {\dfrac{{\sqrt 3 }}{2}L} \right)^2} = \dfrac{1}{4}M{L^2}$
This equivalent to AC also
$\Rightarrow MI = 0 + \dfrac{1}{4}M{L^2} + \dfrac{1}{4}M{L^2}$
Hence,
$\Rightarrow MI = \dfrac{1}{2}M{L^2}$

Hence option A is the right option.

Note: The torque required for acceleration about the rotational axis is determined by moment of inertia. The sum of moment of inertia of each rod is the moment of inertia of the system. Moment of inertia is also called rotational inertia. The moment of inertia gives the relationship for the dynamic of rotational motion.