Question
Question: Three identical thin rods, each of mass \(m\) and length \(l\) are joined to form an equilateral tri...
Three identical thin rods, each of mass m and length l are joined to form an equilateral triangle. The moment of inertia of the triangle about one of its sides is given as,
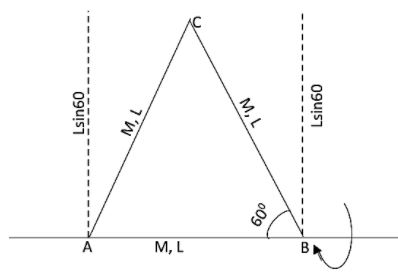
Solution
The moment of inertia of the system is the sum of moment of inertia of each rod. The rod at the axis will not be having the moment of inertia, as the distance is zero. Angles at which the rod is aligned with respect to the axis also has to be taken care of. These all may help you to solve this question.
Complete step-by-step answer:
First of all let us find out the total moment of inertia of the system. This can be found out by using the sum of the moment of inertia of each rod. This can be written as,
MI=IAB+IBC+IAC
Here when we examine the figure, we can see that the rod AB is perfectly kept at the axis. As this is in the axis, its moment of inertia will be zero. This is because the distance between the axis and the rod will be zero.
MI=31ML2=0
Now let us look at the BC and AC. They are having the same kind of arrangement about the axis.
Therefore the moment of BC is found by the equation,
MI=31MLeff2
Where M be the mass of the rod, Leff be the effective length or the distance between the rods.
Here the effective length is the perpendicular length to the axis which is given as,
Leff=Lsinθ
Where θbe the angle of the equilateral triangle. This angle is equal to,
θ=60∘
Therefore after substituting the values in it, the effective length will be,
Leff=Lsin60∘=23L
Therefore the moment of inertia of the rod will be
MI=31MLeff2
Substituting the effective length in this equation will give,
MI=31M(23L)2=3×43ML2=41ML2
This will be equivalent for the rod AC also. Therefore the total effective length will be given as,
MI=0+41ML2+41ML2MI=21ML2
Therefore the answer has been obtained.
Note: The moment of inertia of a body is defined as the quantity which determines the torque required for a needed acceleration about the rotational axis. This is otherwise referred to as mass moment of inertia or the rotational inertia. This is analogous to the mass in classical physics.
