Question
Question: Three identical thin rods, each of length \(L\) and mass \(m\) , are welded perpendicular to one ano...
Three identical thin rods, each of length L and mass m , are welded perpendicular to one another as shown in figure. The assembly is rotated about an axis that passes through the end of one rod and is parallel to another. Determine the moment of inertia of this structure about this axis.
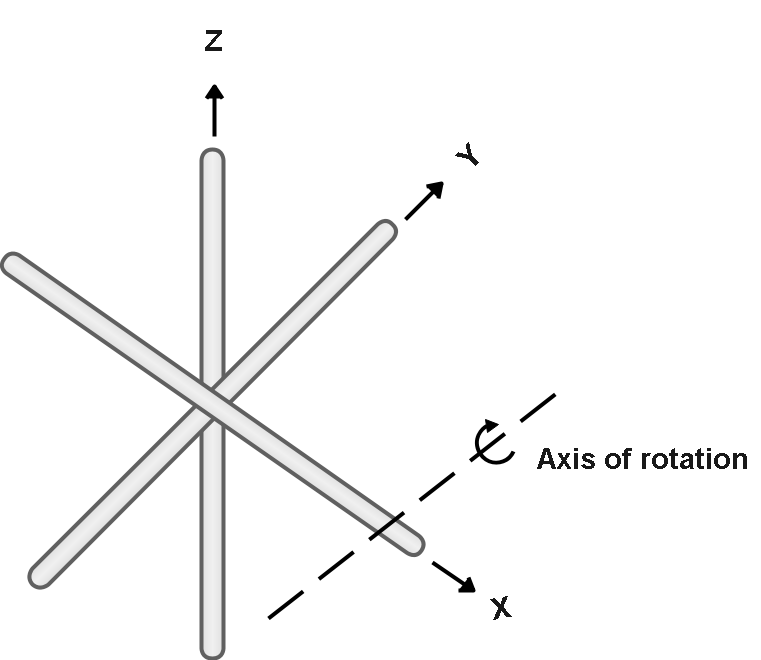
Solution
To answer this type of question, first we will find the moment of inertia about the centre of the mass and then by using parallel axis theorem we will find the required moment of inertia of the structure about the given axis.
Complete step by step solution:
According to the question,
There are three identical rods.
Mass of each rod is m and
Length of each rod is L .
As, the axis of rotation is parallel to the Y-axis and is at the distance of 2L from the centre of the system of rods where the total mass of the system is located.
So, moment of inertia of the rod along X-axis about Y- axis passing through the centre is I1=12mL2 .
Now, the moment of inertia of the rod along y-axis about y-axis is I2=0 (axis through centre, parallel to the rod because the rod is thin.)
And, Moment of inertia of the rod along Z-axis about Y -axis is I3=12mL2
Y-axis is at a distance of x=2L ,from the given axis of rotation,
Now, by parallel axis of theorem,
We know that the moment of inertia of the system of rods is moment of inertia of system about y-axis and (mass of system) (square of distance between origin and axis of rotation)
i.e.,
Hence the moment of inertia of the given structure is 1211mL2 .
Note:
The torque required for acceleration about the rotational axis is determined by moment of inertia. The sum of moment of inertia of each rod is the moment of inertia of the system. Moment of inertia is also called rotational inertia. The moment of inertia gives the relationship for the dynamic of rotational motion.
