Solveeit Logo
Login

Question

Question: Three identical stars, each of mass M, form an equilateral triangle (stars are positioned at the cor...

Three identical stars, each of mass M, form an equilateral triangle (stars are positioned at the corners) that rotates around the center of the triangle. The system is isolated and the edge of the triangle is L. The amount of work done, that is required to dismantle the system is:
A.GM22L\dfrac {G{M}^{2}} {2L}
B.3GM22L\dfrac {3G{M}^{2}} {2L}
C.3GM24L\dfrac {3G{M}^{2}} {4L}
D.3GM2L\dfrac {3G{M}^{2}} {L}

Explanation

Solution

Firstly, use the formula for gravitational potential energy of the system. Multiply the energy by 3 as there are 3 stars. Divide this obtained potential energy by 2 to get the total energy. As in circular motion, potential energy is twice the total energy in the system. Negative energy will be required to dismantle the system, hence, negate the obtained total energy. This obtained energy will be the amount of work done to dismantle the system.
Formula used:
P.E.=−N×Gm1m2RP.E.= -N \times \dfrac {G{m}_{1}{m}_{2}}{R}
P.E.=2EP.E.=2E

Complete answer:
Given: Number of particles (N) =3
Particles have same mass (m1=m2=m3)=M({m}_{1} ={m}_{2}={m}_{3})= M
Distance (R) = L
Gravitational potential energy of the system is given by,
P.E.=−N×Gm1m2RP.E.= -N \times \dfrac {G{m}_{1}{m}_{2}}{R}
∴P.E.=−3×GM2L\therefore P.E.=-3 \times \dfrac {G{M}^{2}} {L} ...(1)
In uniform circular motion, potential energy is given by,
P.E.=2EP.E.=2E ...(2)
Where, E is the total energy in the system
Rearranging equation. (2) we get,
⇒E=P.E.2\Rightarrow E= \dfrac {P.E.}{2}
Substituting equation. (1) in above equation we get,
⇒E=−3×GM22L\Rightarrow E= -3 \times \dfrac {G{M}^{2}} {2L}
Energy required to dismantle the system is equal to -E.
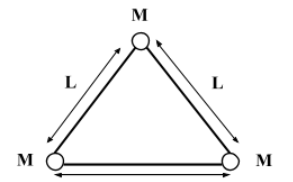
∴Energyrequired=3×GM22L\therefore Energy \quad required=3 \times \dfrac {G{M}^{2}} {2L}

Thus,the amount of work done that is required to dismantle the system is 3GM22L\dfrac {3G{M}^{2}} {2L}.

Hence, the correct answer is option B i.e. 3GM22L\dfrac {3G{M}^{2}} {2L}.

Note:
If the system was at some height then the equation would have changed. Gravitational potential energy of the system at height his given by,
P.E.=−N×Gm1m2R+hP.E.= -N \times \dfrac {G{m}_{1}{m}_{2}}{R+h}
In the above equation, h is the height from the surface of the earth and not from the center of the earth.
If you consider the height from the center of the earth then the equation would change to,
P.E.=−N×Gm1m2R−hP.E.= -N \times \dfrac {G{m}_{1}{m}_{2}}{R-h}