Question
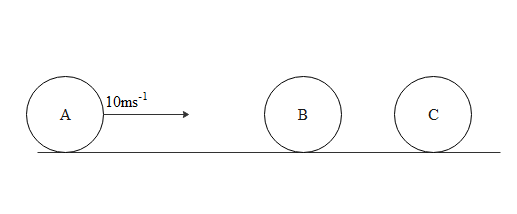
Question: Three identical spherical balls A, B, C are placed on a table as shown in the figure along a straigh...
Three identical spherical balls A, B, C are placed on a table as shown in the figure along a straight line. B and C are at rest initially. The ball A hits B head on with a speed of 10ms−1. Then after all collisions (assumed to be elastic) A and B are brought to rest and C takes off with a velocity of
A. 5ms−1
B. 10ms−1
C. 2.5ms−1
D. 7.5ms−1
Solution
In case of collisions whether they are elastic or inelastic collisions there is always one thing we conserve which is momentum. If those collisions are elastic then we will conserve kinetic energy too. In case of inelastic collisions we can’t conserve the kinetic energy because it is lost in the form of heat or sound.
Formula used:
\eqalign{
& p = mv \cr
& {p_i} = {p_f} \cr}
Complete step by step answer:
According to Newton's second law as long as there is no external impulsive force momentum will always be conserved. For example if a bomb or rock explodes then we can conserve the momentum because explosion is considered as an internal reaction. So when there is no external impulsive force we find out the momentum of the rock or bomb before it gets exploded and we equate it to the momentum of the system of pieces after the rock has exploded. In this we solve many problems.
Now coming to the given question first the ball A collides with B and comes to rest
We have momentum p=mv where ‘m’ is the mass and ‘v’ is the velocity
We conserve the momentum for this collision pi=pf
Initial momentum before collision is pi=m×10=10m
Final momentum after collision will be of mass B only as mass A comes to rest pf=mv where ‘v’ is the velocity of mass B because A comes to rest after collision and it doesn’t contribute to final momentum
pi=pf
\eqalign{
& \Rightarrow 10m = mv \cr
& \Rightarrow 10 = v \cr}
Now coming to next step the ball B collides with C and comes to rest
We have momentum p=mv where ‘m’ is the mass and ‘v’ is the velocity
We conserve the momentum for this collision pi=pf
Initial momentum before collision is pi=m×10=10m
Final momentum after collision will be of mass C only as mass B comes to rest pf=mv where ‘v’ is the velocity of mass C because B comes to rest after collision and it doesn’t contribute to final momentum
pi=pf
\eqalign{
& \Rightarrow 10m = mv \cr
& \Rightarrow 10 = v \cr}
So velocity of sphere C will be 10ms−1
Hence answer would be option B.
Note:
During the collision there is an external force which is gravity but still we had conserved the momentum because gravity is not the external impulsive force and collision is the very short time action and within that time gravity doesn’t create much difference to the momentum of the system.
