Question

Three identical spheres, each of mass $1kg$ are placed touching each other with their centres on a straight line. Their centres are marked P, Q and R respectively. The distance of centre of mass of the system from P is:
A) $\dfrac{{PQ + PR + QR}}{3}$
B) $\dfrac{{PQ + PR}}{3}$
C) $\dfrac{{PQ + QR}}{3}$
D) $\dfrac{{PR + QR}}{3}$

Answer 1

All the three spheres are identical and the spheres are touching each other. The mass of each sphere is given as $1kg$ . Use the formula to calculate the centre of mass. Put the values of distance as the distances between the centres of the spheres. The total mass of the system is $3kg$ .

Complete step by step solution: The center of mass is the average position of all the particles of the system. Any force acting on the system is supposed to be acting at this point.
In order to answer this question, let us draw an appropriate figure for the same.

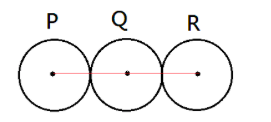
It is given that the mass of each sphere is $1kg$ .
We need to find the centre of mass from P.
The line joining the centres is parallel to the horizontal, so the centre of mass will also lie in the horizontal direction only.
The formula to calculate the center of mass is given as:

$x = \dfrac{{{m_p}({x_p}) + {m_Q}({x_Q}) + {m_R}({x_R})}}{{{m_p} + {m_Q} + {m_R}}}$
Here, $x$ is the centre of mass from point P.

${m_p},{m_Q},{m_R}$ are the mass of each sphere, we have ${m_p} = {m_Q} = {m_R} = 1kg$
${x_p},{x_Q},{x_R}$ are the distances from point P, we have;
${x_p} = 0$ , ${x_Q} = PQ$ and ${x_R} = PR$ .

Substituting these values in the above equation, we get

$x = \dfrac{{1(0) + 1(PQ) + 1(PR)}}{{1 + 1 + 1}}$
$\Rightarrow x = \dfrac{{PQ + PR}}{3}$

The centre of mass lies at a distance of $\dfrac{{PQ + PR}}{3}$ from point P.

Therefore, option B is the correct option.

Note: In some cases, the center of mass may also lie outside the body. We were not given with the value of the distances between two spheres thus, we left the answer in terms of variables. The center of mass will be different from points Q and R. The center of mass also depends on the mass of the body but in this case the mass was $1kg$ .