Question
Question: Three identical rods, each of mass m and length l, form an equilateral triangle. Moment of inertia a...
Three identical rods, each of mass m and length l, form an equilateral triangle. Moment of inertia about one of the sides is
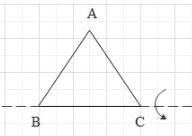
A. 4ml2B. 2ml2C. 43ml2D. 32ml2
Solution
To solve this question we need to use the concept of moment of inertia. Since, the rods in the triangle are of equal length, the angles in the triangle are also equal. Find the effective length of the rod about the axis of rotation. Then use the moment of inertia formula to find the moment of inertia of each of the rod and then add them to find the total moment of inertia of the system.
Complete answer:
The moment of inertia of the system can be found by finding the moment of inertia of each rod in the system.
Now, a moment of inertia of the system is needed about one of the sides made by the rod of the triangle.
The rods of which the triangle is made of are of equal length and equal mass. Since, the length of the rods are equal, the triangle formed is an equilateral triangle and the angle of the triangle formed are also equal and each of the angle is equal to 600
Now, the total moment of inertia of the system will be equal to the moment of inertia of each roda in the triangle.
Mathematically we can express it as,
I=IAB+IBC+ICA
Now, the moment of inertia due to the rod BC is zero, because the axis of rotation of the triangle is in BC itself.
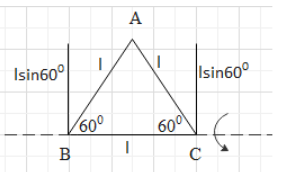
Now, the moment of inertia of the rod AB and BC can be found out as,
IAB=31mleff2=31m(lsin600)2IAB=31ml2(23)2IAB=41ml2
Similarly,
ICA=41ml2
So, the total moment of inertia of the system will be,
I=41ml2+0+41ml2I=21ml2
The correct option is (B).
Note:
For different objects the moment of inertia can be different. The moment of inertia of a body depends on the shape and size of the body and also depends on the position of the axis of rotation of the object.
