Question
Question: Three identical Polaroid sheets \({P_1}\) , \({P_2}\) and \({P_3}\) are oriented so that the pass ax...
Three identical Polaroid sheets P1 , P2 and P3 are oriented so that the pass axis of P2 and P3 are inclined at angles of 60∘ and 90∘ respectively with the pass axis of P1 . A monochromatic source S of unpolarised light of intensity is kept in front of the Polaroid sheet P1 , as shown in the figure. Determine the intensities of light as observed by the observer at O, when Polaroid P3 is rotated with respect to P2 at an angle 30∘ and 60∘.
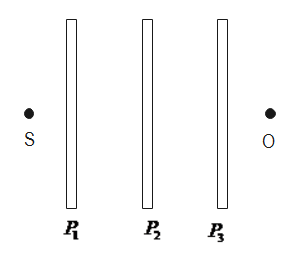
Solution
In this question we will use the relation between the intensity and the angle made by the Polaroid. Further, by using the given condition, we will get the required result. We will also study the basics of intensity, wave and propagation of waves.
Formula used:
I=I0cos2θ
Complete step by step solution:
As we know that, the intensity of radiant energy is defined as the power transferred per unit area. Here the area is measured on the plane perpendicular to the direction of propagation of the energy or wave. Further, intensity can be calculated as the square of the given amplitude.
Here as we know that the ray of light passing through Polaroid P1 will have intensity reduced by half, which will be given as:
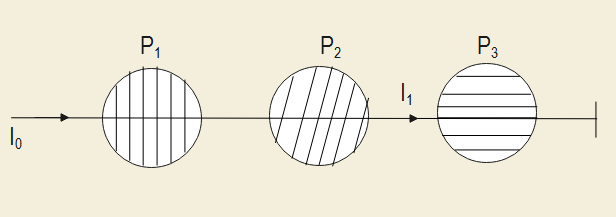
I1=2I0
Now, the Polaroid P1 is oriented at an angle 60∘ with respect to P2. So, we get the intensity as:
I2=I1cos260∘
By, substituting the given values, we get:
I2=2I0×41
⇒I2=8I0
Now, the Polaroid P3 is oriented at an angle 30∘ with respect to P1 . So, when we rotateP3 at 30∘, the angle betweenP2 andP3 is 60∘. Here, we get the intensity as:
I3=I2cos260∘
By, substituting the given values, we get:
I3=8I0×41
⇒I3=I+320
Similarly when P3 is rotated by 60∘, the angle between P2 and P3 is 90∘. So, the intensity we get:
I3=I2cos290∘
By, substituting the given values, we get:
\eqalign{& {I_3} = \dfrac{{{I_0}}}{8} \times 0 \cr
& \therefore {I_3} = 0 \cr}
Therefore, we get the required result, that give us the intensities of light as observed by the observer at O, when Polaroid P3is rotated with respect to P2 at an angle 30∘ and 60∘
Additional information:
Waves involve the transfer of energy without the transfer of the matter. So, it can be said that waves can be described as a disturbance that travels through a medium, transporting energy from one location to another location without transfer of matter.
Further, the frequency is defined as the number of waves that pass a fixed point in unit time. It can also be defined as the number of cycles or vibrations undergone during one unit of time.
Two waves are said to be coherent if they are moving with the same frequency and have constant phase difference.
The summation or adding or subtraction of all the waves travelling in a particular medium, gives us the superposition of waves. If the direction or amplitude of the waves are opposite then the superposition of waves is calculated by subtracting the waves, whereas if the two waves are travelling in the same direction or have same amplitude the resultant is given by adding up the two or more waves.
The S.I unit of frequency is Hertz or Hz and the unit of wavelength is meter or m. Furthermore we also know the S.I unit of time which is given by second or s.
Phase of a wave specifies the location of a point within a wave cycle of a repetitive waveform. Generally, the phase differences between two or more sound waves are important.
Note:
The phase of the wave can be positive or negative depending on its direction of propagation. A sine wave starts from zero, whereas the cosine wave starts from one. A wave which has the same amplitude but opposite orientation will cancel out each other and thereby give zero output.
