Question

Three identical point masses, each of mass $1\,kg$ lie in the x-y plane at points $\left( {0,0} \right)$ ,$\left( {0,0.2\,m} \right)$ and $\left( {0.2\,m,0} \right)$ . The gravitational force on the mass at the origin:
A. $1.67 \times {10^{ - 9}}\left( {\widehat i + \widehat j} \right)N$
B. $3.34 \times {10^{ - 10}}\left( {\widehat i + \widehat j} \right)N$
C. $1.67 \times {10^9}\left( {\widehat i - \widehat j} \right)N$
D. $3.34 \times {10^{10}}\left( {\widehat i - \widehat j} \right)N$

Answer 1

Gravitational force occurs between two bodies. But in the question, there are 3 point particles involved. So to find the gravitational force, take two-point masses at a time, solve it and add to get the final result. Also, remember to mention the direction of force as it is a vector quantity. Draw the diagram first according to the given coordinates to get a visual representation.

Complete step by step solution:
Sir Isaac Newton formulated the law of universal gravitation to explain the gravitational force. The law states that every particle in the universe attracts every other particle with a force that is directly proportional to the product of the masses and inversely proportional to the square of the distance between them. Mathematically, it can be represented as:
$F \propto \dfrac{{{m_1} \times {m_2}}}{{{r^2}}}$
$\Rightarrow F = G.\dfrac{{{m_1} \times {m_2}}}{{{r^2}}}$
Where,
$F$ = Gravitational force in Newton
${m_1}$ and ${m_2}$ = masses of the bodies in kilograms
$r$ = distance between the masses in meters
$G$ = Gravitational constant
The value of $G$ is $6.67 \times {10^{ - 11}}N.{m^2}.k{g^{ - 2}}$ .

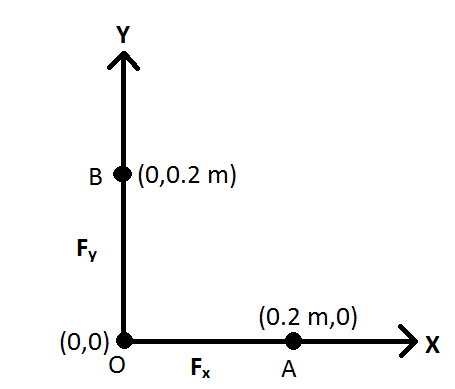
The data given in the question are as follows:
${m_1} = {m_2} = {m_3} = 1kg$
${r_x} = 0.2\,m$
${r_y} = 0.2\,m$
where ${m_1} =$ mass at the origin
${m_2} =$ mass at X-axis
${m_3} =$ mass at Y-axis
${r_x} =$ distance between the mass at origin and mass at X-axis
${r_y} =$ distance between the mass at origin and mass at Y-axis
First, consider the particles at origin and X-axis and find the gravitational force, ${F_x}$ at the origin due to the particle placed at X-axis:
${F_x} = G.\dfrac{{{m_1} \times {m_2}}}{{{r_x}^2}}\,\widehat {\,i}$
$\Rightarrow {F_x} = \dfrac{{6.67 \times {{10}^{ - 11}} \times 1 \times 1}}{{{{\left( {0.2} \right)}^2}}}\,\,\widehat i$
$\Rightarrow {F_x} = \dfrac{{6.67 \times {{10}^{ - 11}} \times 1 \times 1}}{{0.04}}\,\,\widehat i$
$\Rightarrow {F_x} = \dfrac{{6.67 \times {{10}^{ - 11}} \times 1 \times 1}}{{{{\left( {0.2} \right)}^2}}}\,\,\widehat i$
$\Rightarrow {F_x} = 1.67 \times {10^{ - 9}}\,\widehat i\,\,N$
Now, consider the particles at origin and Y-axis and find the gravitational force, ${F_y}$ at the origin due to the particle placed at Y-axis:
${F_y} = G.\dfrac{{{m_1} \times {m_3}}}{{{r_x}^2}}\,\widehat j$
$\Rightarrow {F_y} = \dfrac{{6.67 \times {{10}^{ - 11}} \times 1 \times 1}}{{{{\left( {0.2} \right)}^2}}}\,\,\widehat j$
$\Rightarrow {F_y} = \dfrac{{6.67 \times {{10}^{ - 11}} \times 1 \times 1}}{{0.04}}\,\,\widehat j$
$\Rightarrow {F_y} = \dfrac{{6.67 \times {{10}^{ - 11}} \times 1 \times 1}}{{{{\left( {0.2} \right)}^2}}}\,\,\widehat j$
$\Rightarrow {F_y} = 1.67 \times {10^{ - 9}}\,\widehat j\,\,N$
The total force, $F$ on the particle at origin, is given by:
$F = {F_x} + {F_y}$
$\Rightarrow F = \,\left( {1.67 \times {{10}^{ - 9}}\,\widehat i\, + \,1.67 \times {{10}^{ - 9}}\,\widehat j} \right)\,N$
$\Rightarrow F = 1.67 \times {10^{ - 9}}\,\left( {\widehat i + \widehat j} \right)\,N$
The direction of the force ${F_x}$ is along the positive X direction as we have to find the direction of the force exerted by a particle on the X-axis on the particle at the origin. Similarly, the direction of force ${F_y}$ is along the positive Y direction. $\widehat i$ and $\widehat j$ are the unit vectors of the X-axis and Y-axis which represent the direction. Unit vectors are those vectors whose magnitude is equal to $1$ and has a particular direction. Mathematically, it is represented by:
$\widehat a = \dfrac{{\overrightarrow a }}{{\left| {\overrightarrow a } \right|}}$
Therefore, option A is the correct answer.

Note:
Gravitational force is the weakest known force in nature and hence can often be neglected when strong forces act on an object. The weight measured by human beings is actually the gravitational force exerted by the earth on the body. The acceleration gained by a freely falling object is called the acceleration due to gravity. It is different in different places and hence, the weight also differs because weight is proportional to acceleration due to gravity.