Question

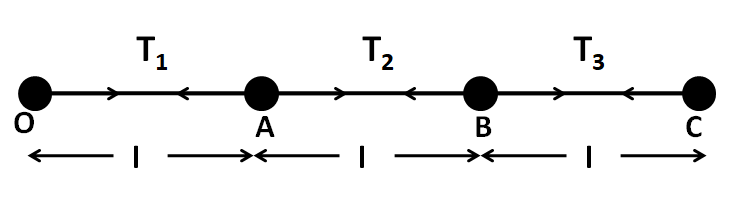
Three identical particles are joined together by a thread as shown in figure. All the three particles are moving on a smooth horizontal plane about point O. If the speed of the outermost particle is ${v_0}$ then the ratio of tensions in the three sections of the string is: (Assume that the string remains straight)

(A) $3:5:7$
(B) $3:4:5$
(C) $7:11:6$
(D) $3:5:6$

Answer 1

Hint To solve this question, we need to identify the motion of the particles given in the question. Then, using Newton’s second and third law of motion, we can obtain the required ratio.

Formula Used: The formula used here is given by
$\Rightarrow F = \dfrac{{m{v^2}}}{r}$ , here $F$ is the centripetal force acting on a particle of mass $m$ which is moving with the velocity $v$ in a circle of radius $r$ .
$\Rightarrow v = \omega r$ , here $v$ is the speed of a particle moving in a circle of radius $r$ with an angular velocity of $\omega$ .

Complete step by step answer
Let ${T_1}$ , ${T_2}$ , and ${T_3}$ be the respective tensions in the threads OA, AB, and BC, as shown in the below

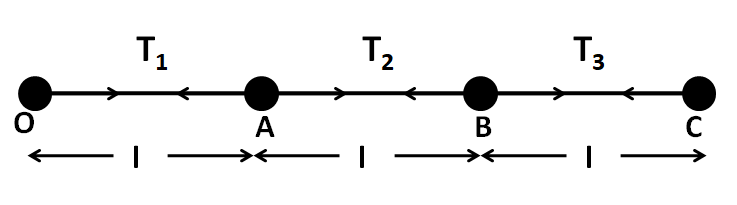
Since all the particles are connected by the thread which remains straight throughout their motion, so the distance between the particles remains constant, or in other words, there is no relative motion between the objects. As all the particles move about the point O, therefore the only possible motion of the particles is the circular motion, which has its centre is at the point O.
Let the angular velocity of the particles be $\omega$ .
So the velocity of A is
$\Rightarrow {v_A} = \omega \times OA$
$\Rightarrow {v_A} = \omega l$ ………………………..(1)
The velocity of B is
$\Rightarrow {v_B} = \omega \times \left( {OA + AB} \right)$
$\Rightarrow {v_B} = 2\omega l$ ………………………….(2)
And the velocity of C is
$\Rightarrow {v_C} = \omega \times \left( {OA + AB + BC} \right)$
$\Rightarrow {v_C} = 3\omega l$ ……………………….(3)
Now consider the free body diagram of the particle C

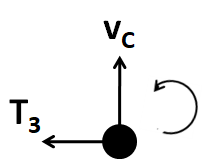
As this particle is moving in a circle of radius $3l$ , so the force of tension ${T_3}$ provides the required centripetal force, that is
$\Rightarrow {T_3} = \dfrac{{m{v_c}^2}}{{3l}}$
From (3)
$\Rightarrow {T_3} = \dfrac{{m{{\left( {3\omega l} \right)}^2}}}{{3l}}$
$\Rightarrow {T_3} = 3m{\omega ^2}l$ ……………………..(4)
Now, considering the free body diagram of B

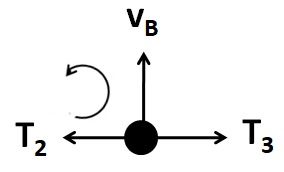
This particle is moving in a circle of radius $2l$ , so we get
$\Rightarrow {T_2} - {T_3} = \dfrac{{m{v_B}^2}}{{2l}}$
Putting (2) and (4) we get
$\Rightarrow {T_2} - 3m{\omega ^2}l = \dfrac{{m{{\left( {2\omega l} \right)}^2}}}{{2l}}$
$\Rightarrow {T_2} = 5m{\omega ^2}l$ ………………………...(5)
Finally, considering the free body diagram of A

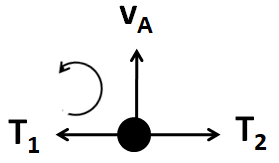
As this particle is moving in a circle of radius $l$ , so we have
$\Rightarrow {T_1} - {T_2} = \dfrac{{m{v_A}^2}}{l}$
Putting (1) and (5)
$\Rightarrow {T_1} - 5m{\omega ^2}l = \dfrac{{m{{\left( {\omega l} \right)}^2}}}{l}$
$\Rightarrow {T_1} = 6m{\omega ^2}l$ ………………...(6)
From (4), (5) and (6), we get
$\Rightarrow {T_3}:{T_2}:{T_1} = 3m{\omega ^2}l:5m{\omega ^2}l:6m{\omega ^2}l$
On simplifying we get
$\Rightarrow {T_3}:{T_2}:{T_1} = 3:5:6$
Hence, the correct answer is option D.

Note
The speed of the outermost particle, which is given in the question, is not required to solve this question. This is because ultimately we need to take the ratio of all the three forces of tension. So it doesn’t matter in the form of which variables are these forces expressed. Do not try to include the speed ${v_0}$ in your solution, as it will unnecessarily increase the calculations.