Question

Three identical particles are joined together by a thread as shown in figure. All the three particles are moving in a horizontal plane. If the velocity of the outermost three particles is ${v_0}$ then the ratio of tension in the three sections of the string is

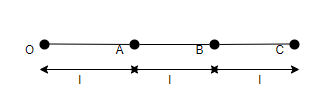
A. $3:5:7$
B. $3:4:5$
C. $7:11:6$
D. $3:5:6$

Answer 1

Here we will proceed by using the concept of angular speed which is denoted by $\omega$ known as omega. Then we can find out the ratio of tension in the three sections of the string.

Formula used:
$v = \omega \times r$
Where, $v$ is velocity, $\omega$ is angular speed, $r$ is radius

Complete step by step answer:
We know that $r = L$ (Given)
Assume the mass of each ball is $m$.
Ray diagram for showing the tension between the balls is given below,

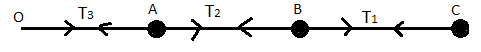
For the ball C, ${v_0} = \omega 3L$
From here, $\omega = \dfrac{{{v_0}}}{{3L}}$, angular speed is same for all the three balls because the angular displacement is same in the same time of motion.
For ball A force due to rotation on it is $= m{\omega ^2}L = m\dfrac{{{v_0}^2}}{{9L}}$
For ball B force due to rotation on it is $= m{\omega ^2}2L = \dfrac{{2m{v_0}^2}}{{9L}}$
For ball C force due to rotation on it is $= m{\omega ^2}3L = \dfrac{{m{v_0}^2}}{{3L}}$
Tension in the string joining the ball B and C ${T_1} = \dfrac{{m{v_0}^2}}{{3L}}$
Tension in the string joining the ball A and B ${T_2} = \dfrac{{2m{v_0}^2}}{{9L}} + \dfrac{{m{v_0}^2}}{{3L}} = \dfrac{{5m{v_0}^2}}{{9L}}$
Tension in the string joining the ball O and A
${T_3} = \dfrac{{m{v_0}^2}}{{9L}} + \dfrac{{2m{v_0}^2}}{{9L}} + \dfrac{{m{v_0}^2}}{{3L}} = \dfrac{{2m{v_0}^2}}{{3L}}$
Now, ${T_1}:{T_2}:{T_3} = \dfrac{{m{v_0}^2}}{{3L}} \& :\dfrac{{5m{v_0}^2}}{{9L}}:\dfrac{{2m{v_0}^2}}{{3L}}$
$\Rightarrow \dfrac{1}{3}:\dfrac{5}{9}:\dfrac{2}{3}$
Now in the first and third fraction multiply 3 to the numerator and denominator of each fraction $= 9$
$\Rightarrow {T_1}:{T_2}:{T_3} = \dfrac{{1 \times 3}}{{3 \times 3}}:\dfrac{5}{9}:\dfrac{{2 \times 3}}{{3 \times 3}} \\\ = \dfrac{3}{9}:\dfrac{5}{9}:\dfrac{6}{9} \\\$
Now, since the denominator of each fraction is same it will be cancelled from all the three fractions so you will get ${T_1}:{T_2}:{T_3} = 3:5:6$
Therefore, option D is the correct answer.

Note:
Whenever we come up with this type of question, one must know that Angular speed refers to how quickly an object is rotating. It is defined as the change in angle of the object per unit of time. It is measured in radians. By using this concept it should be easier to solve questions related to angular velocity.