Question
Question: Three identical particles are joined together by a thread as shown. All the three particles are movi...
Three identical particles are joined together by a thread as shown. All the three particles are moving in a horizontal plane. If the velocity of the outermost particle is v0 then the ratio of tensions in the three sections of the string is
A. 3:5:6
B. 3:4:5
C. 7:11:6
D. 3:5:7
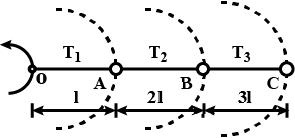
Solution
Hint: As all the three particles are moving together in a horizontal plane. The angular velocity for all the particles is equal. We shall substitute the length of each particle in the tension formula and their ratio gives the answer.
Complete step by step answer:
The physical objects that are in contact will exert forces on each other. This force can be called by different names. If one of the objects exerting force is like a string or rope or thread, we can call the force as tension. It is also known as an action reaction pair of forces acting at the end of elements. The expression to calculate tension can be written as
T=mω2l
Where, ‘m’ is the mass of the object
‘ω’ is the angular velocity and
‘l’ is the distance of the particles from the origin
As the three particles are identical, they have the same mass and angular velocity.
The tension of particles can be calculated as
Tc=mω2(3l)
TB=Tc+mω2(2l)=mω2(5l)
TA=TB+mω2(l)=mω2(6l)
Let us now calculate the ratios
Tc:TB:TA=3:5:6
Therefore, the correct answer for the given question is option (A).
Note: Tension is the pulling force and not pushing force as threads or strings cannot push effectively, trying to push a thread can cause them to lack tension. This must be remembered when illustrating the force on an object. It is also known as the opposite of compression force. The unit of tension force is Newton (N).
