Question

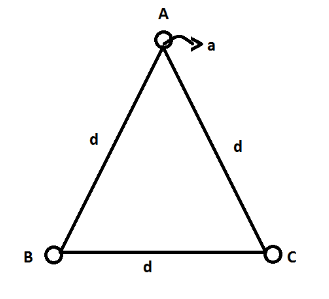
Three identical metallic uncharged spheres $A,{\text{ }}B,{\text{ }}and{\text{ }}C$ each of the radius a, kept at the corners of an equilateral triangle of side $d(d \gg a)$ as shown in the figure. The fourth sphere (of radius$a$), which has a change in$q$, touches A and then moves to a position far away. Bis earthed and then the earth connection is removed C is then earthed. The charge on C is:

(A) $\dfrac{{qa}}{{2d}}(\dfrac{{2d - a}}{{2d}})$
(B) $\dfrac{{qa}}{{2d}}(\dfrac{{2d - a}}{d})$
(C) $- \dfrac{{qa}}{{2d}}(\dfrac{{d - a}}{d})$
(D) $\dfrac{{qa}}{{2d}}(\dfrac{{d - a}}{{2d}})$

Answer 1

If a charged metallic sphere contacts the same size of metallic sphere, then half of the charge is transferred to another one.If a metallic sphere is earthed, then the net potential on that sphere has become zero. There is a charge dislocation in the earthed sphere by the influence of other charges nearby.

Complete step by step answer:
Initially, there are no charges in A, B, C, spheres. So-net charge ${q_{net}} = 0$
Then there is a fourth sphere comes in contact with sphere A
So the charge is transferred to A by an amount of $q/2$
${q_A} = q/2$
Then removed the fourth sphere and earthed the B sphere. (Indicates figure B)
Because of earthed net Potential at B, ${V_{net}} = 0$ and there is a charge $q'$ on B.
${V_{net}} = {V_A} + {V_B}$

${V_{net}} = \dfrac{{k{q_A}}}{{{r_A}}} + \dfrac{{k{q_B}}}{{{r_B}}}$
${r_A}$ Distance between centre of the sphere A and centre of the sphere B, ${r_A} = a + d + a = d + 2a$ but $d \gg a$ so ${r_A} = d + 2a = d$.
${V_A}$ Is the potential due to the sphere A.
${V_B}$ Is the potential due to the charge dislocation in B.
$k$ is a constant.
${V_{net}} = \dfrac{{k(q/2)}}{d} + \dfrac{{kq'}}{a} = 0$
$\dfrac{{kq}}{{2d}} = \dfrac{{ - kq'}}{a}$, then $q' = \dfrac{{ - qa}}{{2d}}$this is the charge on B.
Now, earth connection removed from B and earthed C
So, net potential on C =0 $V{'_{net}} = 0$
$V{'_{net}} = {V_A} + {V_B} + {V_C} = 0$
We already know ${V_A}$and ${V_B}$ and substitute values.
$0 = \dfrac{{k{q_{}}}}{{2d}} + \dfrac{{ - kqa}}{{2{d^2}}} + \dfrac{{k{q_C}'}}{a}$
Cancel all $k$
$\dfrac{{k{q_{}}}}{{2d}} + \dfrac{{ - kqa}}{{2{d^2}}} = - \dfrac{{k{q_C}'}}{a}$
$\dfrac{{{q_{}}}}{{2d}} + \dfrac{{ - qa}}{{2{d^2}}} = - \dfrac{{{q_C}'}}{a}$
$(\dfrac{{{q_{}}}}{{2d}} + \dfrac{{ - qa}}{{2{d^2}}})a = - {q_C}'$
The charge on C is
${q_C}' = - \dfrac{{qa}}{{2d}}[\dfrac{{d - a}}{d}]$
So the answer is (C) $- \dfrac{{qa}}{{2d}}(\dfrac{{d - a}}{d})$

Note: Earthed means is the grounding of the metallic sphere. We should count this term $2a$ in $d + 2a$, if this $d \gg a$ is not given. Earthling is used in electrical appliances to prevent electric shock by providing a path of unwanted charge flow.