Question
Question: Three identical metal plates with large surface areas are kept parallel to each other as shown in fi...
Three identical metal plates with large surface areas are kept parallel to each other as shown in figure. The leftmost plate is given a charge Q, the rightmost a charge −2Q and the middle one remains neutral. The charge appearing on the outer surface of the rightmost plate is?
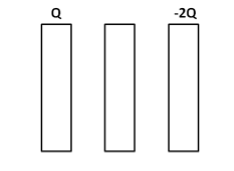
(A) 2Q
(B) 3Q
(C) −2Q
(D) −4Q
Solution
To solve this question, we need to use the theorem of conservation of the charge for getting the charge distribution on the left and the right surfaces of each of the three plates. Then considering the net electric field inside any of the plates equal to zero, we will get the final distribution of charge.
Complete step-by-step solution:
Let the surface area of each of the plates be A.
Let the charge on the outer surface of the rightmost plate be q. Since the rightmost plate carries a total charge of −2Q, so the charge on its inner surface becomes −(2Q+q). Now, due to the negative charge on the inner surface of the rightmost plate, equal positive charge will get induced on the surface present on the right side of the middle plate. So the charge present on the right side surface of the middle plate is equal to (2Q+q). Since the middle plate is neutral, an equal amount of negative charge will get induced on its left side surface. So the charge present on the left surface of the middle plate becomes equal to −(2Q+q). Proceeding this way, we get the charge on the inner surface of the leftmost plate equal to (2Q+q), and that on its outer surface equal to −(Q+q).
So the charge distribution on the plates can be represented as in the figure below.
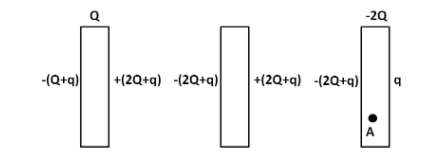
Now, we consider the electric field at a point A within the last plate, as shown in the above figure.
Each surface of a metal plate can be treated as an infinite sheet. We know that the electric field due to an infinite sheet is given by
E=ε0σ
Therefore, the net electric field at A can be given by
EA=Aε0−(Q+q)+Aε0(2Q+q)−Aε0(2Q+q)+Aε0(2Q+q)−Aε0(2Q+q)−Aε0q
⇒EA=Aε0−(Q+2q)
Now, we know that the electric field inside a metal is equal to zero. Therefore we have
EA=0
⇒Aε0−(Q+2q)=0
On solving we get
q=−2Q
Therefore, the charge appearing on the outer surface of the rightmost plate is equal to −2Q.
Hence, the correct answer is option C.
Note: The surface area of the plates is given to be large in the question. Therefore we could assume either side of each plate to be an infinite sheet.
