Solveeit Logo
Login

Question

Question: Three identical charges, each having a value \( 1.0 \times {10^{ - 3}}C \) are placed at the corners...

Three identical charges, each having a value 1.0×10−3C1.0 \times {10^{ - 3}}C are placed at the corners of an equivalent triangle of side 20cm20cm . Find the potential at the center of the triangle.
(A) 2.3×106V2.3 \times {10^6}V
(B) 2.3×105V2.3 \times {10^5}V
(C) 2.3×104V2.3 \times {10^4}V
(D) 2.3×103V2.3 \times {10^3}V

Explanation

Solution

Hint : Firstly, find the distance between the corner and the center. After finding the distance we can use the formula for the electric field because we are already provided with the value of charge and the length of the triangle. The formula of electric field is E=14πε0QRE = \dfrac{1}{{4\pi {\varepsilon _0}}}\dfrac{Q}{R} .

Complete Step By Step Answer:
Consider a triangle ABCABC as shown in the diagram. OO is the center of the triangle on which we have to find the potential. Given that identical charges are placed at the corners each having value 10−3C{10^{ - 3}}C and the sides of length 20cm20cm .
Revising the concepts for electric potential, which is defined as the amount of work needed to move a unit charge from reference point to specific point against the electric field.
To Find distance OBOB we are taking the right-angled triangle ABDABD

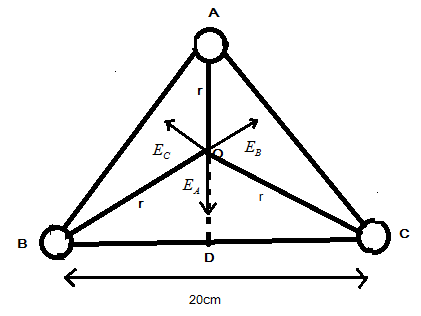
Using Pythagoras theorem,
(AB)2=(BD)2+(AD)2{\left( {AB} \right)^2} = {\left( {BD} \right)^2} + {\left( {AD} \right)^2}
(20×10−2)2=(10×10−2)2+(AD)2{\left( {20 \times {{10}^{ - 2}}} \right)^2} = {\left( {10 \times {{10}^{ - 2}}} \right)^2} + {\left( {AD} \right)^2}
In this above statement we had taken the BD=BC2BD = \dfrac{{BC}}{2} because the centroid always bisects the base of the triangle. On calculating,
AD=1.732×10−2mAD = 1.732 \times {10^{ - 2}}m
Now finding the rr which is comes to the two-third of the side ADAD
r=23(1.732×10−2)=1.15×10−1r = \dfrac{2}{3}\left( {1.732 \times {{10}^{ - 2}}} \right) = 1.15 \times {10^{ - 1}}
Now simply substituting the values in the formula for electric potential:
V=9×109×1×10−31.15×10−1V = 9 \times {10^9} \times \dfrac{{1 \times {{10}^{ - 3}}}}{{1.15 \times {{10}^{ - 1}}}}
Total potential comes out to be
V=3×9×109×10−3+1  \begin{gathered} V = 3 \times 9 \times {10^9} \times {10^{ - 3 + 1}} \\\ \\\ \end{gathered}
Hence the answer is approximately 2.3×108V2.3 \times {10^8}V .

Note :
Electric field at the center is zero due to identical charge placed at the corners of the triangle. This implies that unit positive charge experiences zero electric force. The potential is not zero at the center, that means work has to be done by an external agent to move the unit positive charge from infinity to the center of the triangle.