Question

Three identical cells, each of $4V$ and internal resistance $r$, are connected in series to a $6ohm$ resistor. If the current flowing in the circuit is $2A$.The internal resistance of each cell is.

Answer 1

First we need to calculate the total emf of the tree cells as each emf is given in the problem. Then we have to calculate the total resistance where we add both all the external and internal resistance present in the circuit. Current is given to us using ohm’s law we can calculate the internal resistance of each cell.

Complete step by step answer:
As per the given problem we have three identical cells, each of $4V$ and internal resistance $r$, are connected in series to a $6ohm$ resistor. If the current flowing in the circuit is $2A$.
Now we need to calculate the internal resistance of each cell.

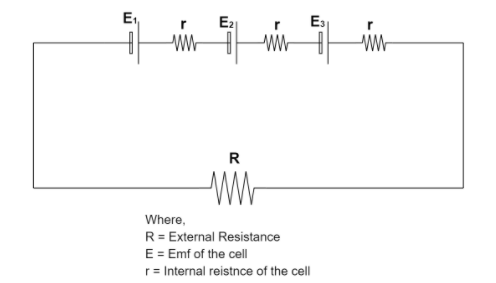
Each emf of the three cell is given as,
$E = {E_1} = {E_2} = {E_3} = 4V$
As all the three are identical cells.
Hence the total emf of the their cell will be,
${E_T} = 3 \times E$
Putting the value of each emf we will get,
${E_T} = 3 \times 4V$
$\Rightarrow {E_T} = 12V$
Now the total resistance of the circuit will be,
External resistance $6ohm$ and the internal resistance $r$ of the cells are connected in series with each other.
If one of the cells has internal resistance as $r$ the three such similar internal resistance will be $3r$.
Applying total resistance formula of the series external and internal resistance will be,
${R_T} = {R_{EXT}} + {R_{INT}}$
Putting the respective values we will get,
${R_T} = \left( {6 + 3r} \right)ohm$
Now applying ohm’s law in the total emf and resistance of the circuit, if the current flowing in the circuit is $2A$ we will get,
${E_T} = I{R_T}$
Putting the known values in the above equation we will get,
$12V = 2A \times \left( {6 + 3r} \right)\Omega$
Taking $2A$ to other side we will get,
$\dfrac{{12V}}{{2A}} = \left( {6 + 3r} \right)\Omega$
$\Rightarrow 6\Omega = \left( {6 + 3r} \right)\Omega$
Taking RHS $6\Omega$ to LHS we will get,
$6\Omega - 6\Omega = 3r\Omega$
$\Rightarrow 3r\Omega = 0$
Hence the value of internal resistance of each of the cells is zero.

Note:
As the internal resistance of the cell we get as zero means there is no internal resistance present in the circuit. Remember that the internal resistance is defined as the opposition to the flow of current that is offered by the cells and which is resulting in the generation of heat. That’s why internal resistance of the cell must be negligible.