Question

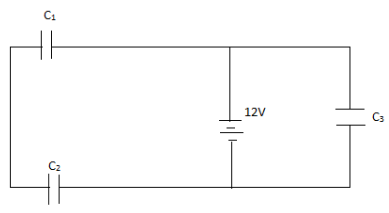
Three identical capacitors ${C_1},{C_2},{C_3}$ of capacitance $6\mu F$ each are connected to a $12V$ battery as shown. Find $\left( i \right)$ charge on each capacitor, $\left( {ii} \right)$ equivalent capacitances of the network, $\left( {iii} \right)$ energy stored in the network of capacitors.

Answer 1

Hint : In order to solve this question, we are going to find the equivalent capacitance for the capacitors ${C_1}$ and ${C_2}$ , the charge on the capacitors is found from the equivalent capacitance and the voltage, then, for ${C_3}$ also, charge is found. Then equivalent capacitance is found for the capacitors in series and the one parallel with them and the energy stored from the equivalent capacitance.
The effective capacitance of the two capacitances ${C_1}$ and ${C_2}$ in series is
${C_{12}} = \dfrac{{{C_1} \times {C_2}}}{{{C_1} + {C_2}}}$
Charge on the capacitor
$q = CV$
And the energy stored is calculated as
$U = \dfrac{1}{2}{C_{eq}}{V^2}$

Complete Step By Step Answer:
Here in this question, we are given the two capacitors ${C_1}$ and ${C_2}$ are connected in series having a potential difference of $12V$ across them and the third ${C_3}$ , having potential difference of $12V$ across it.
The effective capacitance of the two capacitances ${C_1}$ and ${C_2}$ in series is
${C_{12}} = \dfrac{{{C_1} \times {C_2}}}{{{C_1} + {C_2}}}$
Putting the values of the capacitances ${C_1}$ and ${C_2}$ i.e. $6\mu F$
${C_{12}} = \dfrac{{6 \times 6}}{{6 + 6}} = \dfrac{{36}}{{12}} = 3\mu F$
$\left( i \right)$ Charge on each of capacitors ${C_1}$ and ${C_2}$ is same:
${q_1} = {q_2} = {C_{12}}V = \left( {3\mu F} \right) \times \left( {12V} \right) = 36\mu C$
Charge on the capacitor ${C_3}$ is
{q_3} = {C_3}V \\\ \Rightarrow {q_3} = \left( {6\mu F \times 12V} \right) = 72\mu C \\\
$\left( {ii} \right)$ Now, in order to find the equivalent capacitance of network, we are going to use the formula for equivalent capacitance of the capacitors connected in parallel
{C_{eq}} = {C_{12}} + {C_3} \\\ \Rightarrow {C_{eq}} = 3\mu F + 6\mu F = 9\mu F \\\
$\left( {iii} \right)$ Energy stored in the network
The total energy stored is found by taking the equivalent capacitance and the total voltage across the capacitors
$U = \dfrac{1}{2}{C_{eq}}{V^2}$
Putting the values of the equivalent capacitance and the voltage
We get
\Rightarrow U = \dfrac{1}{2} \times \left( {9 \times {{10}^{ - 6}}} \right) \times {\left( {12} \right)^2} \\\ \Rightarrow U = \dfrac{1}{2} \times 9 \times 144 \times {10^{ - 6}} = 648 \times {10^{ - 6}} \\\ \Rightarrow U = 6.48 \times {10^{ - 4}}J \\\

Note :
It is to be noted that you may think that the three capacitors are in series that may seem on seeing the circuit at first. However, this is not true, the parallel and the series combination of the capacitors here depends upon the orientation of the voltage supply and the voltage division.