Question

Three identical capacitors A, B and C are charged to the same potential and them made to discharge through three resistances ${R_A}$​, ${R_B}$​ and ${R_C}$​, where ${R_A} > {R_B} > {R_C}$​. Their potential difference (V) are plotted against time t, giving the curves 1, 2 and 3. Find the correlations between A, B, C and 1, 2, 3.

(A) $1 \to A$
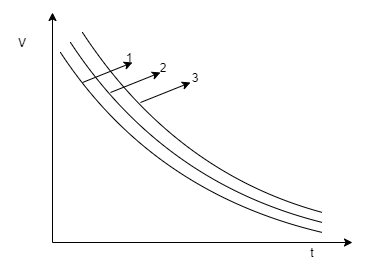
(B) $2 \to B$
(C) $1 \to C$
(D) $3 \to A$

Answer 1

It is given that 3 identical capacitors are charged and discharged through three separate resistances. Now, find the discharge equation of a capacitor and find whether it is related to the resistance value. Using the relation between voltage and resistance, find the correct relation between the capacitor and the resistor.

Complete Step by Step Solution:
Look at the given data. It is stated that 3 capacitors are charged using the same potential V. Now, they are discharged through three resistors, in the order of ${R_A} > {R_B} > {R_C}$. Discharge quotient of a capacitor is the measure of voltage that is getting discharged from a capacitor. Usually, a RC circuit is used for this purpose.as capacitor begins to discharge current through the resistor, the stored energy inside the capacitor is given out with the voltage across the capacitor falling down to zero. The equation used to calculate the discharged voltage is given by,
$\Rightarrow q = {q_0}({e^{\dfrac{{ - t}}{\tau }}})$
where q is the discharged charges from the capacitor, ${q_0}$is the total charge present in the capacitor , t is the time taken for discharge and $\tau$ is the product of capacitance C and resistance R.
Now, we can write charge on the capacitor as the product of its capacitance and the voltage flowing across the capacitor.
$\Rightarrow q = CV$
Substituting this in the above equation, we get,
$\Rightarrow {V_C}C = C{V_0}({e^{\dfrac{{ - t}}{\tau }}})$
Where ${V_C}$is discharged voltage and ${V_0}$is voltage across the capacitor. Cancelling the common term, we get,
$\Rightarrow {V_C} = {V_0}({e^{\dfrac{{ - t}}{{RC}}}})$
This can further be written as ,
$\Rightarrow {V_C} = \dfrac{{{V_0}}}{{{e^{\dfrac{t}{{RC}}}}}}$
So, from this we can see that as R value increases, the exponential value decreases , which subsequently denotes the rise in the discharged voltage value. So, Greater the resistance, greater the voltage discharged.
Graphically, the one with the highest slope will have greater resistance as it has higher current value. Now, curve 3 has the greatest slope than curve 2 and curve 1. So, resistance ${R_A}$corresponds to curve 3. ${R_B}$corresponds to curve 2 and ${R_C}$corresponds to curve 1.

Hence, options (b) (c) and (d) are right answers.

Note: The capacitance of a conductor is defined as the ratio of charge to the voltage supplied to the conductor. Capacitor is a passive device by nature. It starts to get charged when the current flows into it and returns energy to the circuit when the source is disconnected from it.