Question

Three frictionless trolleys are being pulled by a toy engine. The trailing trolley has mass $3\,{\text{kg}}$ The middle trolley has mass $2\,{\text{kg}}$ . The leading trolley has mass $1\,{\text{kg}}$ . If the pulling force is $F = {\text{6}}\,{\text{N}}$ , how much tension $T$ exists in the portion connecting the $3\,{\text{kg}}$ and the $2\,{\text{kg}}$ trolleys?
(A) $0\,{\text{N}}$
(B) $1\,{\text{N}}$
(C) $2\,{\text{N}}$
(D) $3\,{\text{N}}$
(E) $6\,{\text{N}}$

Answer 1

Hint : In this question, the concept of the dynamic force equation is used that is when the system is in motion then the net force applied on the given system is equal to the mass of the whole system times the acceleration of the system. Remember force is a vector quantity and so its direction is also to be taken into account. Such problems can be briskly solved using Newton’s equations of motions.

Complete Step By Step Answer:
In this question, we have given, the pulling force is $F = 6{\text{N}}$ , the mass of the leading trolley is ${m_1} = {\text{1}}\,{\text{kg}}$ , the mass of the middle trolley is ${m_2} = {\text{2}}\,{\text{kg}}$ , and the mass of the trailing trolley is $\;{m_3} = {\text{3}}\,{\text{kg}}$ .
Let us assume the tension in the string between $3\,{\text{kg}}$ and $2\,{\text{kg}}$ be $T$ and the acceleration of the whole system be $a$ .
Let us consider the following diagram of the given system as,

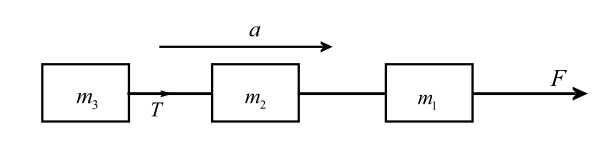
Now we calculate the mass of whole system as,
$M = {m_1} + {m_2} + {m_3}$
Substitute the values of the masses in the above equation,
$\Rightarrow M = {\text{1}} + {\text{2}} + {\text{3}}$
Sum of all masses above equation we get,
$\Rightarrow M = {\text{6}}\;{\text{kg}}$
Now, we write the expression for the acceleration of whole system
$a = \dfrac{F}{M}$
Now we substitute the value of the above formula as,
$\Rightarrow a = \dfrac{6}{6}$
Therefore, after dividing the equation we get,
$\Rightarrow a = {\text{1 m}}/{{\text{s}}^2}$
Now, we calculate the tension for block of mass $3\,{\text{kg}}$ as,
$\Rightarrow T = {m_{\text{3}}}a$
Now, we substitute the value of the mass in the above equation,
$\; \Rightarrow T = {\text{3}} \times {\text{1}}$
Therefore, after the multiply we get the value of $T$ as,
$\therefore T = {\text{3}}\;{\text{N}}$
Thus, the correct option is D.

Note :
The trolley was frictionless, so there is no frictional force. Had frictional force been present, then we would have to take it into account and frictional force always opposes the motion. Newton’s second law is used only when the force is external. If there are internal forces, then as per Newton’s second law, F= 0. While solving such problems involving equations of motion, all the quantities must be taken in standard SI unless specified.