Question

Three forces $\vec P$ , $\vec Q$ and $\vec R$ acting along $IA$ , $IB$ and $IC$ , where $I$ is the incentre of a $\Delta ABC$ , are in equilibrium. Then $\vec P:\vec Q:\vec R$ is:

(A) $\cos \dfrac{A}{2}:\cos \dfrac{B}{2}:\cos \dfrac{C}{2}$
(B) $\sin \dfrac{A}{2}:\sin \dfrac{B}{2}:\sin \dfrac{C}{2}$
(C) $\sec \dfrac{A}{2}:\sec \dfrac{B}{2}:\sec \dfrac{C}{2}$
(D) $cosec\dfrac{A}{2}:cosec\dfrac{B}{2}:cosec\dfrac{C}{2}$

Answer 1

Hint : To solve this question, we need to analyse the properties of incentre. Then we have to apply these properties to get the relation between the lengths and the angles of the triangle given.

Complete step by step answer
We know that the incircle of a triangle is the centre of the circle, known as the incircle which is inscribed in that triangle. Let the radius of the incircle be $k$ .
So, the incentre is shown in the figure below

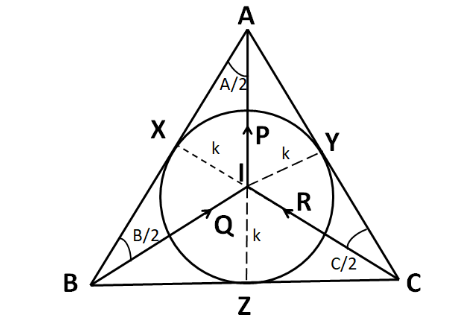
We know that the incentre is the intersection of the angular bisectors of a triangle.
Since all the sides of the triangle are the tangents to the incircle, so the dotted lines shown above are perpendicular to the respective sides.
In triangle BIX, we have
$\Rightarrow \sin \left( {\dfrac{B}{2}} \right) = \dfrac{{IX}}{{IB}}$
$\Rightarrow \sin \left( {\dfrac{B}{2}} \right) = \dfrac{k}{Q}$
So the magnitude of the vector $\vec Q$ is
$\Rightarrow Q = \dfrac{k}{{\sin \left( {\dfrac{B}{2}} \right)}}$
$\Rightarrow Q = kcosec\dfrac{B}{2}$ ……………………….(1)
Now, in triangle CIY we have
$\Rightarrow \sin \left( {\dfrac{C}{2}} \right) = \dfrac{{IY}}{{IC}}$
$\Rightarrow \sin \left( {\dfrac{C}{2}} \right) = \dfrac{k}{R}$
So the magnitude of the vector $\vec R$ is
$\Rightarrow R = \dfrac{k}{{\sin \left( {\dfrac{C}{2}} \right)}}$
$\Rightarrow R = kcosec\dfrac{C}{2}$ ……………………….(2)
Now, in triangle AIX
$\Rightarrow \sin \left( {\dfrac{A}{2}} \right) = \dfrac{{IX}}{{IA}}$
$\Rightarrow \sin \left( {\dfrac{A}{2}} \right) = \dfrac{k}{P}$
So the magnitude of the vector $\vec P$ is
$\Rightarrow P = \dfrac{k}{{\sin \left( {\dfrac{A}{2}} \right)}}$
$\Rightarrow P = kcosec\dfrac{A}{2}$ ……………………….(3)
Now from (1) (2) and (3) we have
$\Rightarrow P:Q:R = kcosec\dfrac{A}{2}:kcosec\dfrac{B}{2}:kcosec\dfrac{C}{2}$
Cancelling out $k$ we get
$\Rightarrow P:Q:R = cosec\dfrac{A}{2}:cosec\dfrac{B}{2}:cosec\dfrac{C}{2}$
Hence, the correct answer is option D.

Note
These types of questions are very much easy, but only if we follow the right approach. And avoiding ourselves from following the wrong approach is even more necessary. For example, if we would have tried to resolve the forces into perpendicular components, then the question would have turned into a disaster. This is because applying the properties of the incentre, and simultaneously working with the components make the question very much complicated. So, it is always recommended to think from the point of view of the information given in the question.