Question

Three forces of magnitudes 6 N, 6 N and 72 N act at the corner of the cube along three sides as shown in figure. Resultant of these forces is:

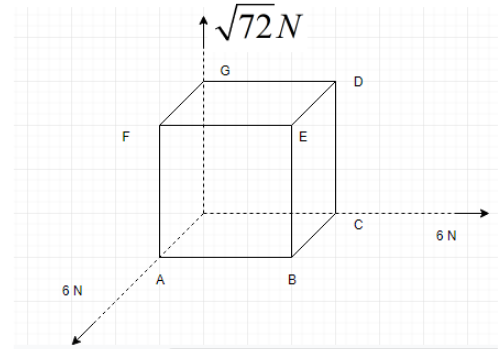
(A) 12N along OB
(B) 18N along OA
(C) 18N along OC
(D) 12N along OE

Answer 1

We can see that there are three forces which are acting along the three coordinate axes. We know that the coordinate axes are mutually perpendicular to each other. So, the angle between $6N$ and $6N$ is ${{90}^{0}}$. The same goes for the other two forces. We can first add any two forces and find out the resultant of the two and that we can add the third force with the resultant to find the net force.

Complete step by step answer:
Let sides OC, OG and OA represent x,y and z respectively.Let us write all the three forces first:
$6\widehat{i},6\widehat{k}$ and $\sqrt{72}\widehat{j}$
First of all, finding the magnitude, adding any two forces,
${{R}_{1}}=\sqrt{{{6}^{2}}+{{6}^{2}}}=6\sqrt{2}N$
Now adding this with the third force we get:
$R=\sqrt{{{(6\sqrt{2})}^{2}}+{{(\sqrt{72})}^{2}}}\\\ \Rightarrow R =\sqrt{72+72}\\\ \Rightarrow R =\sqrt{144}\\\ \therefore R =12N$
So, the resultant of all the three forces is $12N$. Now let us find the direction. Resultant of OA and OC is along OB, this comes directly from parallelogram law.

Therefore, the Resultant of OC, OG and OA will be along OE.

Note: We have used parallelogram law where the two vectors acting at a point are shown based on magnitude and direction, by the two adjacent sides of a parallelogram generated from a particular point and the obtained resultant is represented by the diagonal of the parallelogram that is drawn from the same point. The magnitude of the resultant of the two forces is given by: $R=\sqrt{A{}^\text{2}+B{}^\text{2}+2AB\cos \varphi }$
Where the angle between the forces is $\varphi$.