Question
Question: Three forces each of magnitude F are applied along the edges of a regular hexagon as shown in the fi...
Three forces each of magnitude F are applied along the edges of a regular hexagon as shown in the figure. Each side of the hexagon is a. What is the resultant moment (torque) of these forces about the center O?
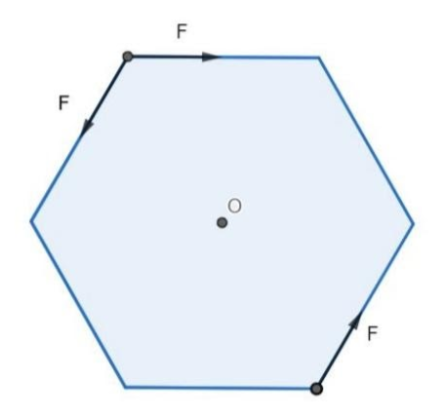
Solution
Find the length of the perpendicular distance between the force and the point O. Calculate the torque by considering the direction also. We can use the formula for the torque which is the sum of products of the force and the perpendicular distance between the point and the force.
Complete step-by-step answer:
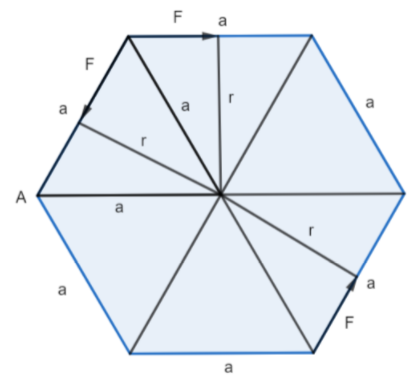
We have a regular hexagon on one side. We know that the length of the diagonal of a regular hexagon is 2a. Then, in the figure, the length of OA is a and the length of OB is a.
Since the lengths AB, OA and OB are equal, the triangle OAB is an equilateral triangle.
Now, we can see that the perpendicular distance between the point O and the force F is r which is the height of the equilateral triangle.
The height of the equilateral triangle with side of length a is given as follows:
r=23a...........(1)
The formula for the torque is the sum of products of the force and the perpendicular distance between the point and the force. It is a vector quantity and has a direction given by the right hand thumb rule.
For the given hexagon, the forces acting in the anti-clockwise direction produce a torque in the anti-clockwise direction and the forces acting in the clockwise direction produce a torque in the clockwise direction.
In the figure, two forces act anti-clockwise and one force act clockwise and they are all at the same distance r from the center O. Hence, the total torque is given as:
T=F.r+F.r−F.r
T=F.r
From equation (1), we have:
T=23Fa (anticlockwise)
Hence, the resultant moment (torque) is 23Fa in the anticlockwise direction.
Note: It is important to consider the direction of the torque in summing them up, since torque is a vector quantity. Sometimes, students add all the torque when they see the term resultant and ignore the direction. This type of silly mistake must be avoided. Also, if we do not know the formula for height of the equilateral triangle, then it will be difficult to solve this question. So, such formulas must be learnt by heart.
