Question

Three forces are acting on a particle of mass, initially in equilibrium. If the first two forces (${R_1}$ and ${R_2}$) perpendicular to each other and suddenly the third force (${R_3}$) is removed, then the acceleration of the particle is:
{\text{A}}{\text{. }}\dfrac{{{R_3}}}{m} \\\ {\text{B}}{\text{. }}\dfrac{{{R_1} + {R_2}}}{m} \\\ {\text{C}}{\text{. }}\dfrac{{{R_1} - {R_2}}}{m} \\\ {\text{D}}{\text{. }}\dfrac{{{R_1}}}{m} \\\

Answer 1

First we should draw a diagram showing the three forces with the first two forces perpendicular to each other. The three forces cancel each other which means that the resultant of any two forces is equal and opposite to the third force and removing one force results in the resultant of the other two forces acting on the particle.

Complete step-by-step answer:

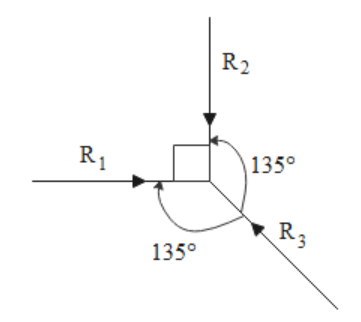
If we diagrammatically visualize the given forces and we get the above diagram. We have three forces ${R_1},{\text{ }}{R_2}$ and ${R_3}$ which act on a particle of mass m in such a way that all the forces cancel each other and the particle stays in equilibrium. The two forces ${R_1}$ and ${R_2}$ are acting on the particle at right angles to each other.
The particle is in equilibrium which means that the three forces cancel each other or more precisely, we can say that the resultant of any two forces cancels the third force. Therefore, we can say that the resultant of forces ${R_1}$ and ${R_2}$ cancels the force ${R_3}$. This implies that the resultant we are talking about is equal in magnitude and in the opposite direction to the force ${R_3}$. This situation can be seen in the following diagram where we have taken the resultant of forces ${R_1}$ and ${R_2}$ to be R and this force is acting in direction opposite to that of the force ${R_3}$.

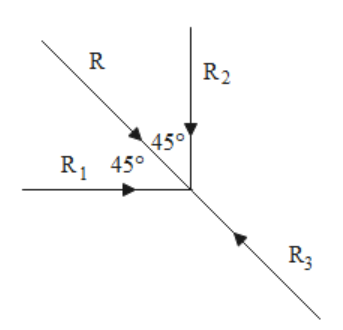
Now if we remove the third force ${R_3}$, the system will lose its equilibrium and only the resultant of forces ${R_1}$ and ${R_2}$ will act on the particle which is R and the magnitude of R is equal to the magnitude of ${R_3}$. Therefore, the acceleration of the particle is given as $\dfrac{{{R_3}}}{m}$. Hence, the correct answer is option A.

Note: The state of equilibrium does not mean that there is nothing happening in the system. It just means that there are forces acting on the system but they all cancel each other leading to zero net motion in the system.