Question

Three forces acting simultaneously on a particle moving with velocity$\vec{V}$. These forces are represented in magnitude and direction by the three sides of a triangle $ABC$(as shown). The particle will now move with velocity:

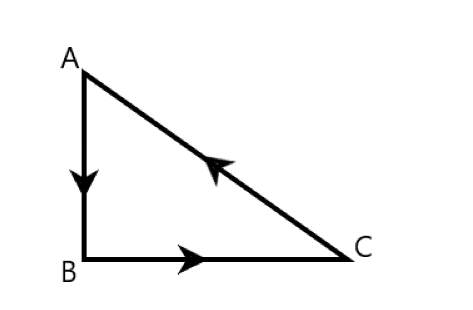
A. Less than$\vec{V}$.
B. Greater than$\vec{V}$.
C. $\left| V \right|$ in the direction of the largest force $BC$.
D. $\vec{V}$remaining unchanged.

Answer 1

As velocity is a vector quantity and we know that vectors have both magnitude and direction, so they cannot be simply added or subtracted algebraically. For finding the resultant of two vectors we use the triangular law of vector addition.

Complete step by step solution:
Triangle law of vector addition states that when two simultaneous vectors are represented as two sides of a triangle with their order of magnitude and direction, then the third vector (third side of triangle) represents the magnitude and direction of the resultant vector in opposite order.

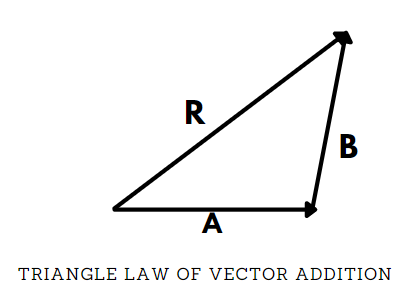
Let, there be two vectors $\vec{A}\,$and$\vec{B}$. To find the resultant vector $\vec{R}$of$\vec{A}\,$and$\vec{B}$. We place$\vec{A}\,$such that the head is at the tail of vector$\vec{B}$and resultant vector$\vec{R}$represents the line joining tail of vector$\vec{A}\,$to the head of vector$\vec{B}$.
Now, the resultant vector$\vec{R}$ is given by vector addition of $\vec{A}\,$and$\vec{B}$ using the triangle law of vector addition.
$\Rightarrow \vec{R}\,=\,\vec{A}\,+\,\vec{B}$
The magnitude of resultant vector is given by$R\,=\,\sqrt{{{A}^{2}}+\,{{B}^{2}}+\,2AB\cos \theta \,}$
The direction of resultant vector is given by $\phi \,=\,{{\tan }^{-1}}\left( \dfrac{B\sin \theta }{A+B\cos \theta } \right)$
Now, according to the question:
Three forces acting simultaneously on a particle moving with velocity$\vec{V}$. These forces are represented in magnitude and direction by the three sides of a triangle $ABC$.

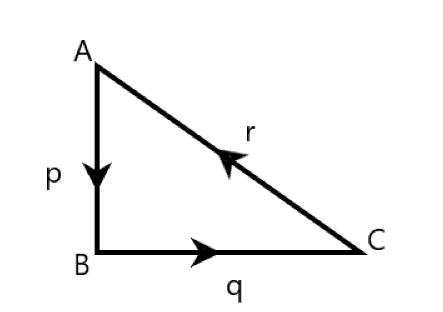
Here,
Vector$\vec{p}$ represents a line joining$AB$.
Vector$\vec{q}$ represents the line joining$BC$.
Vector $\vec{r}$ represents a line joining$CA$.
Since, all three vectors are simultaneous.
Hence, by applying triangle law of vector addition, we get
$\begin{aligned} & \,\,\,\,\,\,\,\vec{p}\,+\,\vec{q}\,=\,-\vec{r} \\\ & \Rightarrow \,\vec{p}\,+\,\vec{q}\,+\,\vec{r}\,=\,0 \\\ \end{aligned}$
$\Rightarrow {{F}_{net}}\,=\,0$
Therefore, the net external force acting on a particle is zero.
Hence, if three vectors are represented by three sides of a triangle taken in the same order, then according to the triangle law of vector addition their resultant is zero. Now, as the resultant of the forces acting on the particle is zero, so the particle's velocity remains unchanged.
Therefore, option (D) $\vec{V}$ remaining unchanged is the correct option.

Note:
If two vectors represented have an angle of 180 degrees or vectors represented are parallel to each other then, we cannot use the triangle law of vector addition. If two vectors act along two adjacent sides of a parallelogram we have to use the parallelogram law of vector addition and the resultants represented by the diagonal of the parallelogram.