Question

Three flat mirrors are arranged mutually perpendicular to each other. The number of distinct images that will be formed due to a point object is?
${\text{A}}{\text{. }}6$
${\text{B}}{\text{. }}7$
${\text{C}}{\text{. }}12$
${\text{D}}{\text{. }}$ None of these.

Answer 1

-The mirrors should be placed like two of them are mutually perpendicular along the sides and the third one is on the top maintaining the right angle with the twos.
-Use the formula of the number of images created if two plane mirrors are at a certain angle.
-When you get the number of images for two mirrors, mind that each of them creates images on the third mirror.
-Since the third mirror is at the top, the one image for the object is also created over there.

Formula used:
The number of images created by consecutive reflection by two mirrors that are placed at an angle $\theta$ is,
$n = \dfrac{{{{360}^0}}}{\theta } - 1$.

Complete step by step answer:
The mirrors are arranged mutually perpendicular to each other. So we can place two of them along the sides at the right angle and the third one is placed on top of the two mirrors maintaining the angle with each of the two mirrors. The arrangement is like the following diagram:

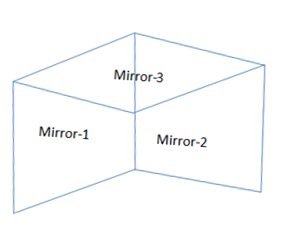
We know that if two mirrors are placed at an angle $\theta$, then the number of the image created by the consecutive reflections by the mirror will be calculated by the following formula,
$n = \dfrac{{{{360}^0}}}{\theta } - 1$, where $n$ = The number of images.
For the Mirror-1 and Mirror-2 the value of $\theta$ is ${90^ \circ }$ ,
Hence, $n = \dfrac{{{{360}^0}}}{{9{0^0}}} - 1$
$\Rightarrow n = 4 - 1$
On subtracting we get,
$\Rightarrow n = 3$
So the number of images for two mirrors along the sides is $3$.
These $3$ images will create other $3$ images at the Mirror-3 placed on the top.
So the total images will be $3 + 3 = 6$.
Since the object is placed in front of the Mirror-1 and Mirror-2, it will create an image on the Mirror-3 placed on the top.
So we can write it as,
The total number of images will be calculated as, $6 + 1 = 7$.
Hence, the right answer is in option $\left( B \right)$

Note: The number of the image created by the consecutive reflections by the mirror will be calculated by the following formula,
$n = \dfrac{{{{360}^0}}}{\theta } - 1$
Here If for a certain angle the value of $n$becomes a fraction number, we should take the next nearest whole number of it as the total number of the image.