Question: Three equal weights of mass 2kg each are hanging on a string over a fixed pulley as shown in the fig...

Question

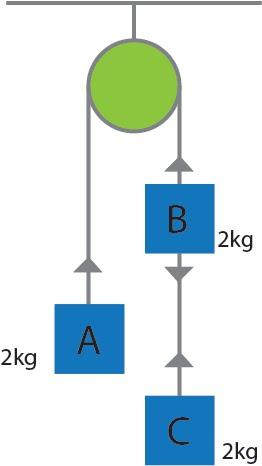
Three equal weights of mass 2kg each are hanging on a string over a fixed pulley as shown in the figure. What is the tension connecting the weights B and C?
A. Zero
B. 13N
C. 30N
D. 19.6N

Answer 1

Solution

Hint: Draw free body diagrams for all the masses and assume an acceleration and resolve the forces for each mass.

Formula used:
$\sum{\text{Force}=\text{mass}}\times \text{acceleration}$

Complete answer step by step:
Let the mass of block A be ${{m}_{a}}=2kg$ MA, mass of block B be ${{m}_{b}}=2kg$ and mass of block C be ${{m}_{c}}=2kg$ ( ${{m}_{a}}={{m}_{b}}={{m}_{c}}=m$ ).Since, mass on the right side of the pulley is greater than the left side, we assume that the system has an acceleration A. Blocks B and C are moving downwards with acceleration $a$ and mass is moving upwards with acceleration $a$ .
Let the tension in the string connecting blocks A and B and blocks B and C be ${{T}_{1}}$ and ${{T}_{2}}$ respectively. Refer to the figure.

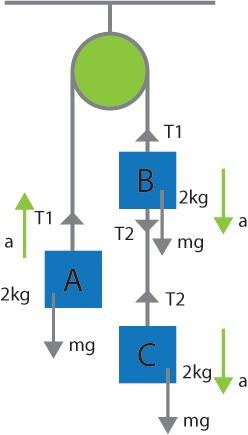
The resultant force acting on a block causes it to accelerate. To describe this, the following expression can be used.
$\sum{\text{Force}=\text{mass}}\times \text{acceleration}$
Therefore, for mass A:
${{T}_{1}}-mg=ma$ …………….(1)
For mass B:
$mg+{{T}_{2}}-{{T}_{1}}=ma$ …………….(2)
For mass C:
$mg-{{T}_{2}}=ma$ ………………….(3)
We have three linear equations in three variables ${{T}_{1}}$ , ${{T}_{2}}$ and $a$ here. We can find values of all the variables by solving them.
Finding expression for ${{T}_{1}}$ from (1)
${{T}_{1}}=mg+ma$
And substituting it in (2)

& \Rightarrow mg+{{T}_{2}}-mg-ma=ma \\\ & \Rightarrow ma=\dfrac{{{T}_{2}}}{2} \\\ \end{aligned}$$ Substituting value of $ma$ in (3) $$\begin{aligned} & \Rightarrow mg-{{T}_{2}}=\dfrac{{{T}_{2}}}{2} \\\ & \Rightarrow {{T}_{2}}=\dfrac{2}{3}mg=\dfrac{2\times 2\times 9.8}{3}\approx 13N \\\ \end{aligned}$$ Therefore, option B. is the correct option. Note: Do not worry if you assumed the initial direction of motion wrong. You will still get the correct answer. But, take care of direction of motion while solving questions with friction on surfaces.