Solveeit Logo
Login

Question

Question: Three equal weights of mass 2kg each are hanging by a string passing over a fixed pulley. The tensio...

Three equal weights of mass 2kg each are hanging by a string passing over a fixed pulley. The tension in the string (in N) connecting B and C is

A

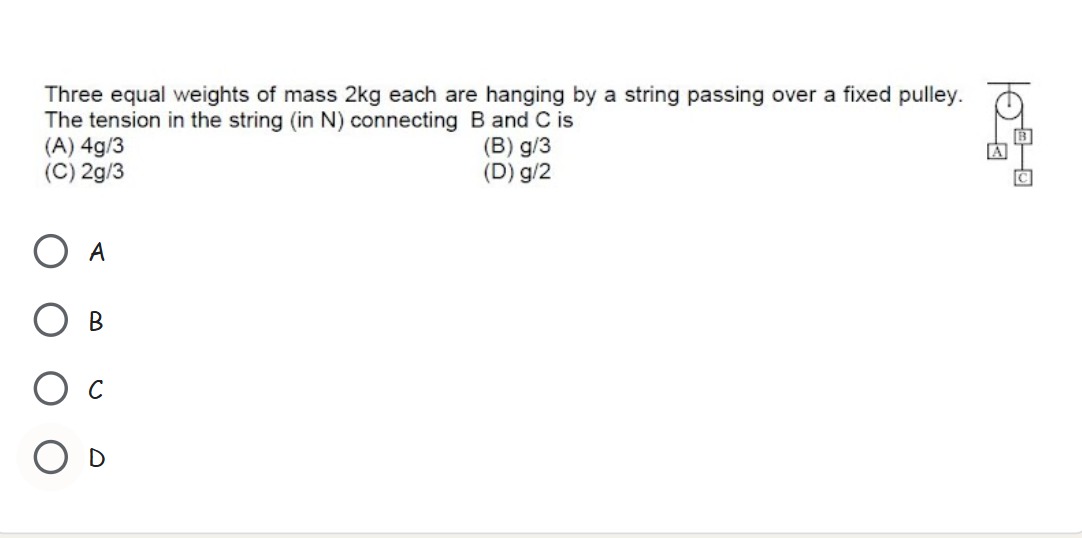
4g/3

B

g/3

C

2g/3

D

g/2

Answer

4g/3

Explanation

Solution

The problem describes a system of three equal weights (A, B, C), each of mass m=2m = 2 kg, connected by strings over a fixed pulley. Block A is on one side, and blocks B and C are stacked on the other side. We need to find the tension in the string connecting B and C.

Let mA=mB=mC=m=2m_A = m_B = m_C = m = 2 kg.

1. Determine the direction of motion and acceleration of the system:

The total mass on the left side of the pulley is ML=mA=mM_L = m_A = m. The total mass on the right side of the pulley is MR=mB+mC=m+m=2mM_R = m_B + m_C = m + m = 2m. Since MR>MLM_R > M_L, the right side of the system (blocks B and C) will accelerate downwards, and the left side (block A) will accelerate upwards. Let the acceleration of the system be aa.

The net force causing the motion is the difference in weights: Fnet=MRg−MLg=2mg−mg=mgF_{net} = M_R g - M_L g = 2mg - mg = mg. The total mass of the system that is accelerating is Mtotal=mA+mB+mC=m+m+m=3mM_{total} = m_A + m_B + m_C = m + m + m = 3m. Using Newton's second law, Fnet=MtotalaF_{net} = M_{total} a: mg=3mamg = 3ma Therefore, the acceleration of the system is a=g3a = \frac{g}{3}.

2. Draw Free Body Diagrams (FBDs) and write equations of motion for each block:

  • Block A (mass mm):

    • Forces:
      • Weight mgmg acting downwards.
      • Tension T1T_1 (in the string over the pulley) acting upwards.
    • Motion: Accelerates upwards with a=g/3a = g/3.
    • Equation of motion: T1−mg=maT_1 - mg = ma T1=mg+ma=mg+m(g3)=mg(1+13)=4mg3T_1 = mg + ma = mg + m\left(\frac{g}{3}\right) = mg\left(1 + \frac{1}{3}\right) = \frac{4mg}{3}.

  • Block C (mass mm):

    • Forces:
      • Weight mgmg acting downwards.
      • Tension T2T_2 (in the string connecting B and C) acting upwards.
    • Motion: Accelerates downwards with a=g/3a = g/3.
    • Equation of motion: mg−T2=mamg - T_2 = ma T2=mg−ma=mg−m(g3)=mg(1−13)=2mg3T_2 = mg - ma = mg - m\left(\frac{g}{3}\right) = mg\left(1 - \frac{1}{3}\right) = \frac{2mg}{3}.

  • Block B (mass mm):

    • Forces:
      • Weight mgmg acting downwards.
      • Tension T1T_1 (from the string over the pulley) acting upwards.
      • Tension T2T_2 (from the string connecting B and C, as C pulls B downwards) acting downwards.
    • Motion: Accelerates downwards with a=g/3a = g/3.
    • Equation of motion: mg+T2−T1=mamg + T_2 - T_1 = ma (This equation can be used to verify consistency, but we have already found T2T_2 from Block C's FBD). Let's verify: mg+2mg3−4mg3=m(g3)mg + \frac{2mg}{3} - \frac{4mg}{3} = m\left(\frac{g}{3}\right) 3mg+2mg−4mg3=mg3\frac{3mg + 2mg - 4mg}{3} = \frac{mg}{3} mg3=mg3\frac{mg}{3} = \frac{mg}{3}. The equations are consistent.

3. Calculate the tension in the string connecting B and C (T2T_2): We found T2=2mg3T_2 = \frac{2mg}{3}. Given m=2m = 2 kg. T2=2×(2 kg)×g3=4g3T_2 = \frac{2 \times (2 \text{ kg}) \times g}{3} = \frac{4g}{3}.

The tension in the string connecting B and C is 4g3\frac{4g}{3} N.