Question
Question: Three equal weights of\(3kg\) each are hanging on a string passing over a frictionless pulley as sho...
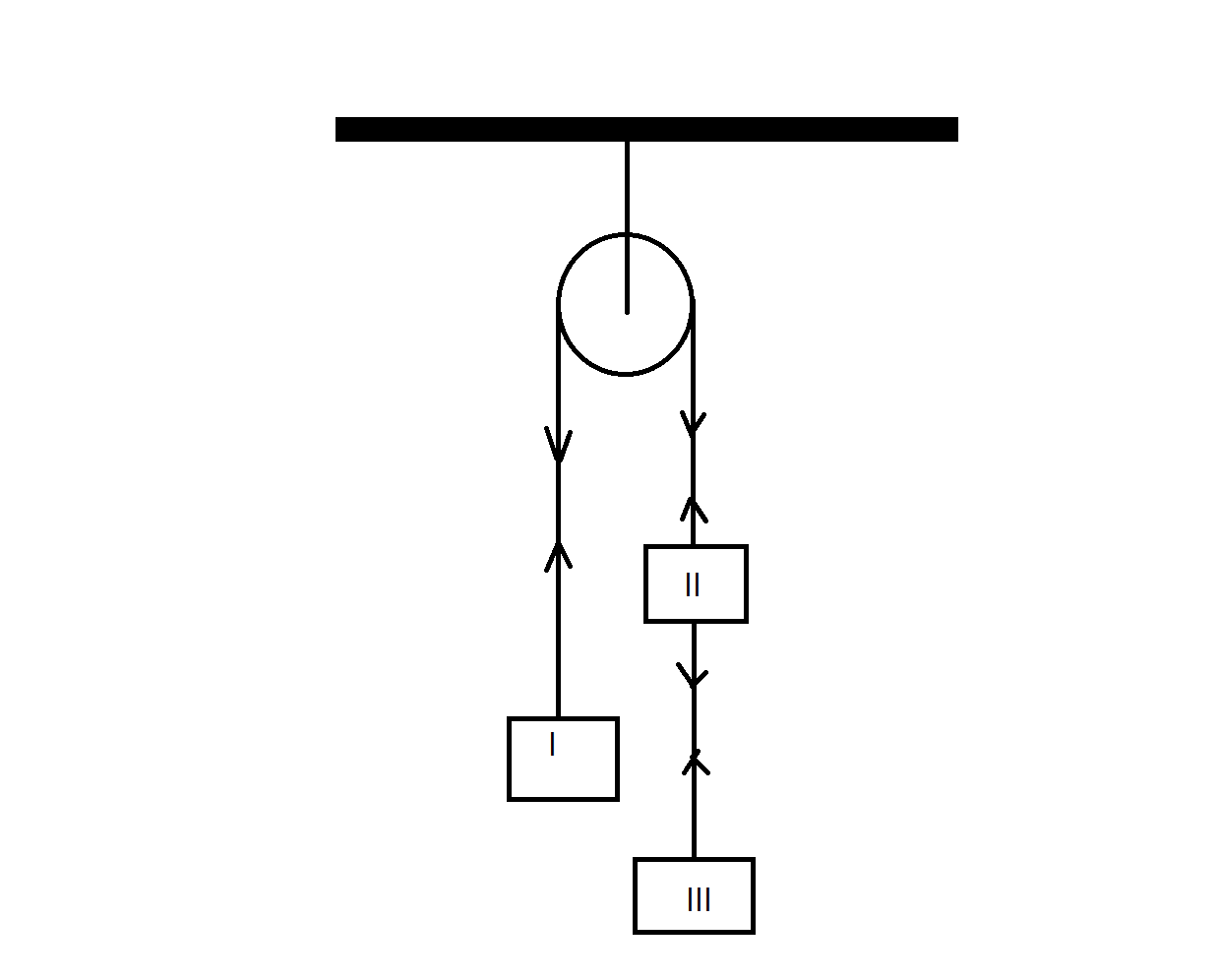
Three equal weights of3kg each are hanging on a string passing over a frictionless pulley as shown in figure. The tension in the string between massesII andIII will be (Takeg=10ms−2)
(A) 5N
(B) 6N
(C) 10N
(D) 20N
Solution
Hint We are given the situation of three blocks of equal masses put up in a certain configuration and are asked to find the tension of the string connecting two of the three blocks. Thus, we will just apply the basics of force and mass configuration.
Complete Step By Step Solution
Here,
For the tension and gravitational force on the blockI, we get
T−mg=ma
Putting the values of mass, we get
T−3g=3a
Thus, we get
T=3a+3g⋅⋅⋅⋅⋅⋅(1)
Now,
For the blocksII andIII, we get
2mg−T=2ma
Putting in the values of mass, we get
6g−T=6a
Further, using equation(1), we get
6g−3a−3g=6a
After further evaluation, we get
3g=9a
Then, we get
a=3g
Now,
The Twe considered till now is the net tension of the string.
Now,
We will take T′ as the tension between the blocksII andIII.
Thus, the equation will be
mg−T′=ma
Further, putting in the values, we get
3g−T′=3a
Further, we get
T′=3g−3a
Thus, putting the evaluated value ofa, we get
T′=3g−3(3g)
Then we get
T′=2g
Putting the value ofg, we get
T′=2×10=20N
Hence, the correct option is (D).
Additional Information The diagram we are considering is called the free body diagram which shows us the bodies and the forces acting on it. The equations we are forming are on the basis of the fundamental idea that all the external forces are in balance for an isolated body.
Note The tension of the string will hold the blocks in equilibrium and will determine the motion of the blocks as the string moves on the pulley. But the tension of the string between the two blocks will make sure that while the motion of the block, the block remains in equilibrium.
