Question

Three equal weights of $3kg$ are hanging on a string passing over a frictionless pulley as shown in the figure. The tension in the string between the masses II and III will be (Take $g=10m/{{\sec }^{2}}$ ):

(A) $5N$
(B) $6N$
(C) $10N$
(D) $20N$

Answer 1

Hint
In the given question, we have been given three weights of equal masses suspended by strings from a pulley. To proceed with the solution, we need to be aware of the fact that in case of a single pulley and string, the acceleration of the objects on either side of the pulley is the same, the difference being that one side goes down and the other side goes up. This happens because a string is inextensible and hence cannot have different acceleration at different points. Let’s move on to see a detailed solution.
$\Rightarrow {{F}_{net}}=ma$

Complete step by step answer
Since the string between masses II and III has no mass of its own, we can consider masses II and III as one system. Now the masses II and III together will have twice the mass as that of mass I, so while mass I come up, the system of masses II and III will go down. What should interest us here is that the tension in the string remains the same because the string has no mass and the acceleration of the two systems of masses also remains the same because the string is inextensible. In the figure given below you can see how we have considered masses II and III as a system and not shown any internal forces.

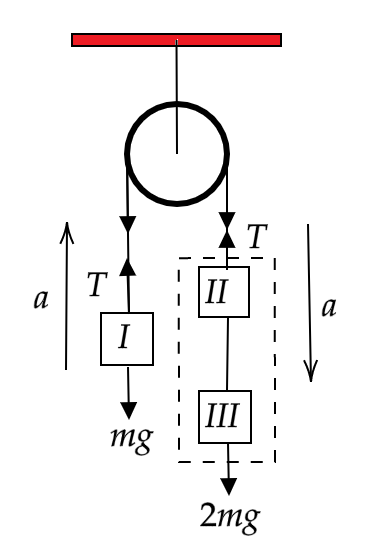
From the figure given above, we can write the force expression for the systems of masses.
For mass I, we have
$\Rightarrow T-mg=ma--equation(1)$ where $T$ is the tension in the string and $mg$ is the weight of the mass acting vertically downwards and $a$ is the acceleration of the block
Refer to the figure for the direction of the acceleration and the direction of the acting forces.
Similarly, for the system of masses II and III, we can write
$\Rightarrow 2mg-T=2ma--equation(2)$ where $T$ is the tension in the string and $2mg$ is the combined weight of the masses acting downwards and $a$ is the acceleration of the system of blocks
Adding the two equations obtained above, we get
$\Rightarrow 2mg-mg=2ma+ma$
$\Rightarrow mg=3ma$
$\Rightarrow a=\dfrac{g}{3}$
Now we can substitute this obtained value of the acceleration in any of the two equations to find the tension in the string.
Substituting the value in $equation(1)$ , we get
$\Rightarrow T-mg=m\times \dfrac{g}{3}$
$\Rightarrow T=\dfrac{4mg}{3}$
Now, considering the system of blocks II and III, we can say that the net force acting on the system must be $2mg-T$ (refer to the figure drawn above)
This net force must be the tension in the strings between the blocks as the system is in equilibrium and hence it cannot be an external force
Hence, tension between the strings of the blocks II and III can be given as $T'$ , where
$\Rightarrow T'=2mg-T$
$\Rightarrow T'=2mg-\dfrac{4mg}{3}=\dfrac{2mg}{3}$
Substituting the value of the mass and the acceleration due to gravity, we get
$\Rightarrow T'=\dfrac{2\times 3\times 10}{3}=20N$.
Hence we can say that option (D) is the correct answer.

Note
Note that we formed the free-body diagrams of the masses and wrote the force equations, and we only substituted the values in the very end. This is advised to avoid confusion in calculations.
Also, we could break the system of masses II and III and then apply a force equation on each of them and reach our solution the old-fashioned way, but we have to act smart and take the best method.