Question: Three equal weights A, B and C of mass 2kg each are hanging on a string passing over a fixed frictio...

Question

Three equal weights A, B and C of mass 2kg each are hanging on a string passing over a fixed frictionless pulley as shown in the figure. The tension in the string connecting weights B and C is:

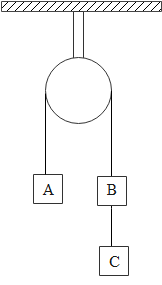
A. Zero
B. 13N
C. 3.3N
D. 19.6N

Answer 1

Solution

Hint: First we need to draw a free body diagram for the given pulley system which shows the various forces acting on the masses hanging on the pulley. Then we need to write various equations of motion for the various blocks using the free body diagram.

Detailed step by step solution:
The free body diagram showing all forces acting on the pulley is as given below:

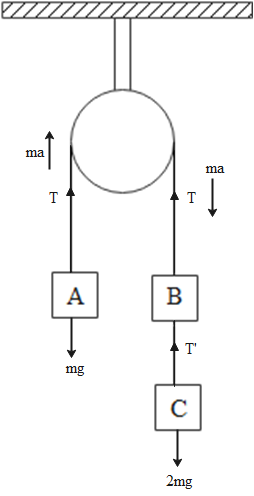
In the diagram, T represents the tension in the string between block A and block B. Between block B and C, the tension is given as T’. The weights of the blocks act in down wards directions as shown.
All blocks weigh the same given as m = 2 kg. The weight is more on the B and C side therefore the block will move upwards and the other two blocks will move downwards. Consider block A first. Depending on the direction of various forces, its equation of motion of terms of various force can be written as
$T + ma = mg \\\ \Rightarrow T = mg - ma \\\ T = 2g - 2a{\text{ }}...{\text{(i)}} \\\$
For system of block B and C together, we have following equation
$2mg + 2ma = T \\\ \Rightarrow 4g + 4a = T{\text{ }}...{\text{(ii)}} \\\$
Solving equation (i) and (ii) simultaneously, we get
$a = - \dfrac{g}{3}{\text{ }}...{\text{(iii)}}$
Now for the single block C, we can write the equation of motion as follows:
$T' = mg + ma \\\ = 2g + 2a \\\$
Using equation (iii) here, we get
$T' = 2g - \dfrac{{2g}}{3} = \dfrac{4}{3}g$
Taking $g = 10m/{s^2}$ , we get tension in the string between B and C to be
$T' = \dfrac{4}{3} \times 10 = 13.33N \simeq 13N$
Hence, the correct answer is option B.

Note: We are given a single fixed pulley which is fixed to the ceiling and the wheel can rotate about the axle. The force applied is in the direction opposite to the direction of motion of the load. Thus pulley helps in reversing the direction of applied force.