Question

Three equal masses of $\;m$ kg each are fixed at the vertices of an equilateral triangle $ABC$.
a. What is the force acting on a mass $2m$ placed at the centroid G of the triangle?
b. What is the force if the mass at vertex A is doubled? Take $AG = BG = CG = 1m$.

Answer 1

Gravitational forces produced by the various regions of the shell have components alongside the line joining the point mass to the center and along a direction perpendicular to this line. The components perpendicular to this line cancels out when totaling over all regions of the shell leaving behind only a resulting force along the line connecting the point to the center.

Complete step by step solution:
Let us take the masses ${m_1},{m_2}$, Gravitational constant $G$ and the distance between them as$l$, where we can get the gravitational force by ${F_G} = G\dfrac{{{m_1} \times {m_2}}}{{{1^2}}}\;$
A. For the first case, From the figure, we can say that the gravitational force $F$ on mass $2m$ at G due to mass at $A$is
${F_1} = G\dfrac{{m \times 2m}}{{{1^2}}} = 2G{m^2}\;$​along $GA$
The gravitational force $F$ on mass $2m$ at $G$ because of mass at$\;B$ is
${F_2} = G\dfrac{{m \times 2m}}{{{1^2}}} = 2G{m^2}\;$along $BG$
The gravitational force $F$on mass $2m$ at because of mass at $C$ is ${F_3} = G\dfrac{{m \times 2m}}{{{1^2}}} = 2G{m^2}\;$along $GC$
Then draw $DE$a parallel to $BC$passing through the point$\;G$. Then$\angle EGC = {30^o} = \angle DGB$.

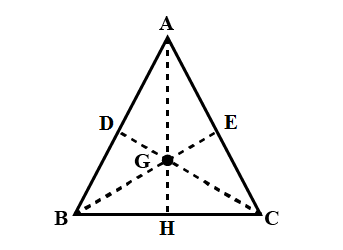
Resolving ${F_2}$​​ and ${F_3}$​​ into two rectangular components, we can get
${F_2}cos{30^{o\;}}$along $GD$and ${F_2}cos{30^{o\;}}$along $GH$
${F_3}cos{30^{o\;}}$along $GE$and ${F_2}cos{30^{o\;}}$along $GH$
Here,${F_2}cos{30^{o\;}}$and ${F_3}cos{30^{o\;}}$are the same in magnitude and acting in reverse directions, and cancel out each other. The resulting force on mass $2m$ at $G$ is
${F_R} = {F_{1}} - \left( {{F_{2}}sin{{30}^o} + {F_{3}}sin{{30}^o}} \right)$
${F_R} = 2G{m^2} - \left( {2G{m^2} \times \dfrac{1}{2} + 2G{m^2} \times \dfrac{1}{2}} \right)$
${F_R} = 0$ this is the required answer
B. For the second case, When mass at $A$ is $2m$, then gravitational force on mass $2m$ at$\;G$ due to mass $2m$ at $A$ is
${F_1} = G\dfrac{{2m \times 2m}}{{{1^2}}} = 4G{m^2}\;$along $GA$
The resulting force on mass $2m$ at $G$ due to masses at$A$,$\;B$ and $C$is
${F_1} = \left( {{F_2}sin{{30}^o} + {F_3}sin{{30}^o}} \right)$
$= 4G{m^2} - \left( {2G{m^2} \times \dfrac{1}{2} + 2G{m^2} \times \dfrac{1}{2}} \right)$
$= 2G{m^2}\;$along $GA$ this is the required answer.

Note:
Every point mass in the extended object will apply a force on the known point mass and these forces will not all be in a similar direction. We have to add up these forces along with their vectors for all the point masses in the extended object to obtain the total force. The force of attraction between a hollow spherical shell of uniform density and a point mass located outside is just as if the total mass of the shell is concentrated at the center of the shell.