Question

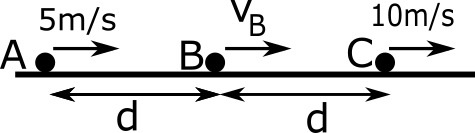
Three elephants A, B and C are moving along a straight line with constant speed in the same direction as shown in figure. Speed of A is $5m/s$ and speed of C is $10m/s$ . Initially separation between A and B is d and between B and C is also d .when B catches C separation between A and C becomes 3d. Then the speed of B will be:

A) $15m/s$
B) $7.5m/s$
C) $20m/s$
D) $5m/s$

Answer 1

We can solve this question by using the relative velocity concept. First we calculate what time distance becomes $3d$ between A and C.
In the same time B catches C it is given then we calculate in what time B catches C and equate the time.

Complete step by step solution:
Step 1
First we calculate in what time separation between A and C become $3d$
Elephant A and B having initial separation $2d$ we assume after time $t$ separation become $3d$ means separation increased by $d$ this distance $d$ will be travel by elephant C with relative velocity with respect elephant A
Relative velocity of elephant C with respect A is ${V_{CA}}$ can be given as
$\Rightarrow {V_{CA}} = {V_C} - {V_A}$
In question given ${V_C} = 10m/s$ and ${V_A} = 5m/s$ put these in above equation
$\Rightarrow {V_{CA}} = 10 - 5 \\\ \Rightarrow {V_{CA}} = 5m/s \\\$
Hence $d$ distance travel in time $t$ with velocity ${V_{CA}}$
We know
velocity=distance x time
$\Rightarrow {V_{CA}} = \dfrac{d}{t} \\\ \Rightarrow 5 = \dfrac{d}{t} \\\$
So time
$\therefore t = \dfrac{d}{5}$ ........ (1)

Step 2
Elephant B catches C in same time in which time separation increase by $d$ between A and C
Elephant B catches C in time $t$ so
Relative velocity of elephant B with respect to C is
$\Rightarrow {V_{BC}} = {V_B} - {V_C}$
$\Rightarrow {V_{BC}} = {V_B} - 10$
With this relative velocity B travel d distance in time $t$
Apply velocity=distance x time
$\Rightarrow {V_{BC}} = \dfrac{d}{t}$
$\Rightarrow {V_B} - 10 = \dfrac{d}{t}$
So time
$\therefore t = \dfrac{d}{{{V_B} - 10}}$ ........ (2)
In question it is given that at the same time B catches C it is given then we calculate in what time B catches C and equate the time.
From equation (1) and (2)
(1)= (2)
$\Rightarrow \dfrac{d}{5} = \dfrac{d}{{{V_B} - 10}}$
Solving this
$\Rightarrow {V_B} - 10 = 5 \\\ \Rightarrow {V_B} = 5 + 10 \\\$
$\therefore {V_B} = 15m/s$
Hence velocity of elephant B is $15m/s$

Hence option A is correct

Note: Here we use relative velocity concept which can be understand as
${V_{AB}} = {V_{AG}} - {V_{BG}}$
Where ${V_{AB}} \Rightarrow$Relative velocity of A with respect to B
${V_{AG}} \Rightarrow$ Velocity of A with respect to ground
${V_{BG}} \Rightarrow$ Velocity of B with respect to ground